图表示学习/图机器学习
CS224W: Machine Learning with Graphs
GuideLines
- Methods for node embeddings: DeepWalk, Node2Vec
- Graph Neural Networks: GCN, GraphSAGE, GAT…
- Graph Transformers
- Knowledge graphs and reasoning: TransE, BetaE
- Generative models for graphs: GraphRNN
- Graphs in 3D: Molecules § Scaling up to large graphs
- Applications to Biomedicine, Science, Technology
Day1:
Node Embedding

Core idea: Embed nodes so that distances in embedding space reflect node similarities in the original network.
对节点进行自动的特征提取-自动嵌入/编码:被下游任务利用
Encoder - Decoder Framework
- encoder 就是node embedding
- decoder 就是对节点vector 做相似度提取:例如内积相似度
随机游走:Random Walk:
思想(Idea)
核心思想是:如果从节点 u 开始的随机游走高概率访问节点 v,那么 u 和 v 是相似的。具体解释如下:
- 访问概率高:从节点 u 开始的随机游走如果高概率访问节点 v,这意味着 u 和 v 之间的路径很多,或者有很多共同的邻居。这说明 u 和 v 在图中的结构位置很相似,具有相似的网络结构特征。
- 多跳信息:随机游走不仅考虑直接的邻居关系,还会通过多跳路径访问更远的节点。这种方式可以捕捉到网络中更复杂的结构信息和节点之间的关系。例如,两个节点即使不直接相连,但如果它们通过多个中间节点有较高的访问概率,那么它们之间仍然具有潜在的相似性。
表达能力(Expressivity)
随机游走路径通过灵活的随机定义方式捕捉节点之间的相似度,能够同时包含局部和高阶的邻域信息:
- 局部信息:随机游走会优先访问与起始节点直接相连的节点,这样能够捕捉节点的局部结构信息。如果两个节点在局部结构上相似(例如,它们有很多共同邻居),那么随机游走路径会较高概率访问到这些共同邻居。
- 高阶信息:随着随机游走的步数增加,它会逐渐扩展到更多的邻居节点,甚至是更远的节点。这样可以捕捉到多跳(multi-hop)的关系信息,即高阶邻域信息。如果两个节点在网络中的更大范围内具有相似的连接模式,随机游走路径也能反映这一点。
随机游走最大化目标节点embedding的对数似然(使得目标节点周围节点的似然概率最大化,原理是周围节点在嵌入向量空间时距离也相对近),这个计算过程可以使用负采样进行优化。
负采样 Negative Sampling:
负采样的原理
负采样的核心思想是用一部分负样本来近似整个负样本空间,从而减少计算开销。具体步骤如下:
- 选择正样本:即实际存在的节点对(例如,图中的实际边)。
- 选择负样本:随机选择一些节点对(图中不存在的边),这些对作为负样本。
负样本数量 (K) 的选择
- 更高的 (K) 值:提供更鲁棒的估计,因为更多的负样本能够更好地近似整个负样本空间。但是这也会增加计算开销。
- 更低的 (K) 值:减少计算开销,但可能会增加对负事件的偏差。
在实际应用中, (K) 通常选择在5到20之间,以平衡计算效率和估计精度。
负样本的选择
负样本可以是任何节点,不一定要与随机游走无关。为了提高效率,常常会从所有节点中随机选择负样本,而不是仅从未在随机游走中出现的节点中选择。
解释负采样公式及其原理
负采样是一种用于提高训练效率和计算效率的方法,尤其是在处理大规模数据集时。下面我们详细解释给定的公式和相关概念。
给定的公式:
$$
\log \left( \frac{\exp(\mathbf{z}_v^\top \mathbf{z}u)}{\sum{n \in N} \exp(\mathbf{z}_n^\top \mathbf{z}_u)} \right) \approx \log \sigma(\mathbf{z}_v^\top \mathbf{z}u) + \sum{k=1}^K \log \sigma(-\mathbf{z}_n^\top \mathbf{z}_u)
$$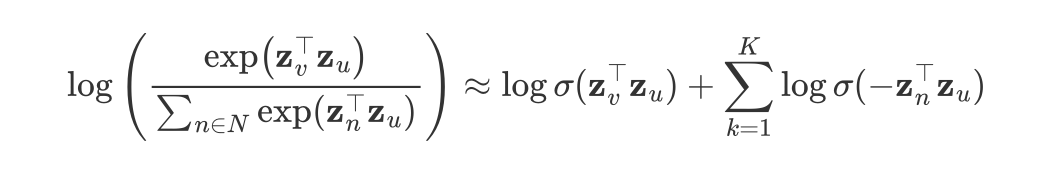
其中:
- $\mathbf{z}_v$ 和 $\mathbf{z}_u$是节点$v$ 和 $u$ 的嵌入向量。
- $\sigma(x)$是sigmoid函数,定义为 $\sigma(x) = \frac{1}{1 + \exp(-x)}$。
- $N$ 是所有节点的集合。
- $K$ 是负样本的数量。
- $\mathbf{z}_n$ 是负样本节点的嵌入向量。
公式表示:
左边的
$$
\log \left( \frac{\exp(\mathbf{z}_v^\top \mathbf{z}u)}{\sum{n \in N} \exp(\mathbf{z}_n^\top \mathbf{z}_u)} \right)
$$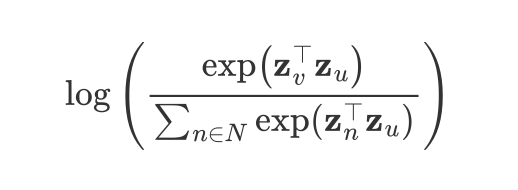
是softmax的对数。
右边的
$$
\log \sigma(\mathbf{z}_v^\top \mathbf{z}u) + \sum{k=1}^K \log \sigma(-\mathbf{z}_n^\top \mathbf{z}_u)
$$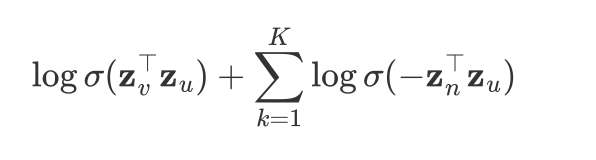
是负采样的对数近似。
==通过负采样,我们可以将计算从整个节点集合的softmax归约到少量负样本的log-sigmoid函数计算,从而大大减少计算复杂度。==
Node Embedding : DeepWalk / Node2Vec
重点内容
DeepWalk:RandomWalk + 词嵌入模型(如Word2Vec)
Node2Vec:DeepWalk + 利用了参数p、q进行BFS/DFS的随机游走,提供了biased的路径选择。
引入了更灵活的随机游走策略,通过调整参数 p 和 q 来控制游走的行为,从而在深度优先搜索(DFS)和广度优先搜索(BFS)之间进行平衡。
利用随机游走得到的node-seq视为word2vec的词序列进行embedding
Limitations:
模型不能推广到训练和测试集中未见过的新节点或新结构:若new node到来,需要重新计算整个graph的node embedding,而不是增量可扩展的。
无法捕捉结构相似性:它们只是用过节点的相邻性来判断空间相似性(距离),而不考虑任何结构信息
主要捕捉的是节点的同质性(homophily)特征,而不是结构相似性(structural similarity)。这意味着它们倾向于将相邻或近邻节点(即在图中距离较近的节点)映射到相似的嵌入空间中,而不是将具有相似结构但在图中距离较远的节点映射到相似的嵌入空间中。
节点同质性假设是指在图中距离较近的节点往往具有相似的特征或属性。例如,在社交网络中,朋友之间的兴趣爱好往往相似。
结构相似性是指两个节点在图中的角色或位置相似,即使它们在图中距离较远。例如,在公司组织图中,两个不同部门的经理可能具有类似的结构角色,即使他们不直接连接。
Solution to these limitations: Deep Representation Learning and Graph Neural Networks
Graph Embedding :图嵌入
Naive:将所有node的嵌入向量进行结合操作(累加/avg/……)
Approach2: 添加一个 上帝虚节点
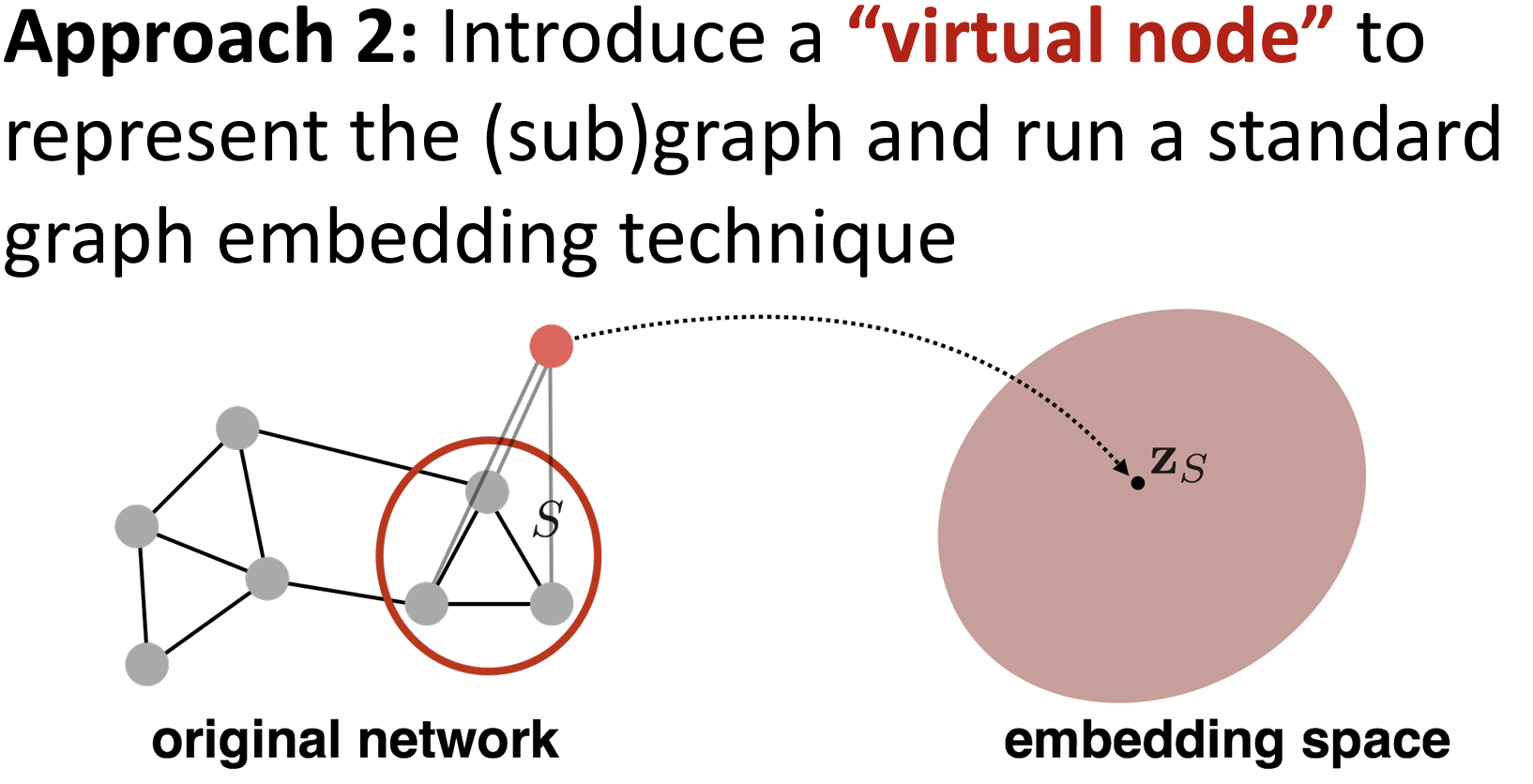
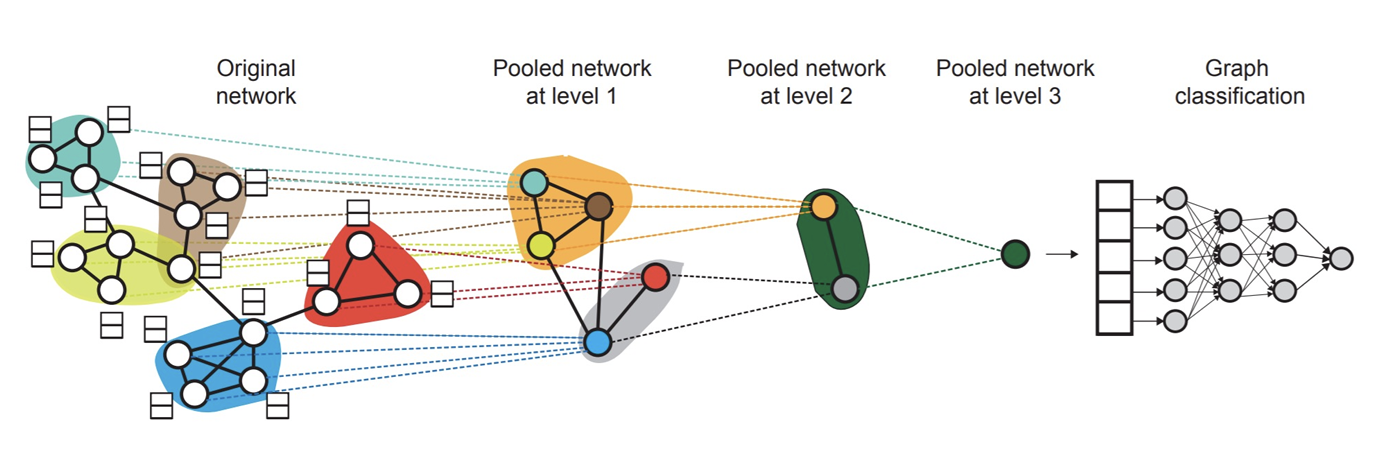
Aprroach3 :分层/pool:DiffPool(Differentiable Pooling)
是一种图神经网络(GNN)池化方法,用于在图上进行层次化聚类,并根据这些聚类对节点嵌入进行求和或平均。
Day1-Lab:
熟悉 NetworkX 以及 PyG 的用法;简单的 NodeEmbedding方法
Day2:
CORE:Graph Neural Network

之前的Node Embedding方法(简单的 encoder - decoder)没有考虑节点结构的信息,只是使用节点距离进行空间嵌入;这里使用GNN深度学习的方法学习节点的嵌入;
Graph vs Image
There is no fixed notion of locality or sliding window on the graph (图上没有固定的局部性或滑动窗口概念)
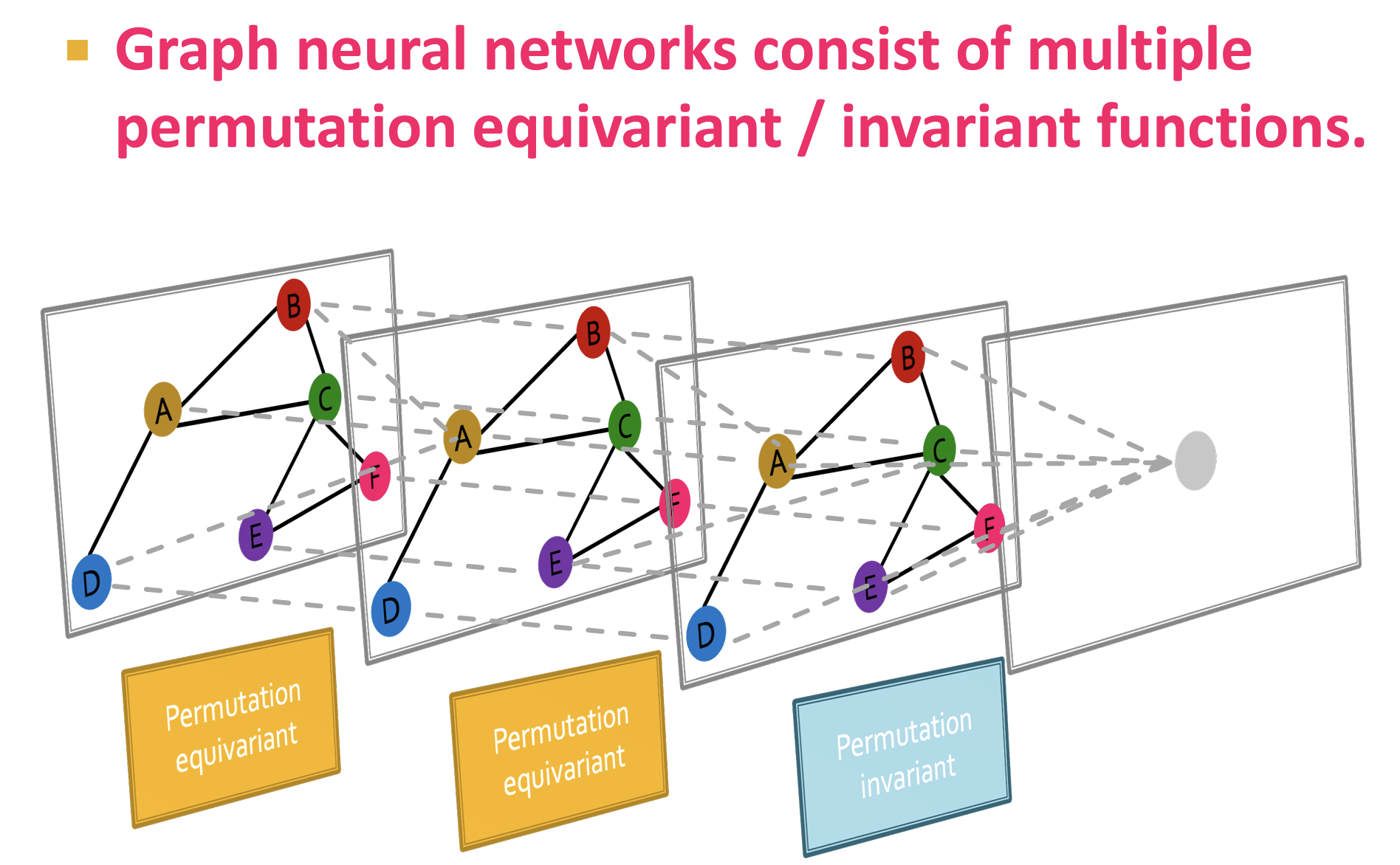
辨析:排列不变性(permutation invariant),不存在一种对节点的权威的排序,任何排序应该有相同的结果;排列等变性(permutation equivariant);
排列不变性意味着,无论图的节点顺序如何,模型的输出结果应该保持不变。假设我们有一个图 $G$,其邻接矩阵为 $A$,节点特征矩阵为 $X$,则排列不变性可以表示为:
$ f(A, X) = f(PAP^T, PX) $
其中,$P$ 是一个任意的排列矩阵,它可以重新排列图的节点。排列不变性的一个例子是将图映射到一个固定长度的向量。无论如何重新排列输入图的节点,输出向量始终保持不变。
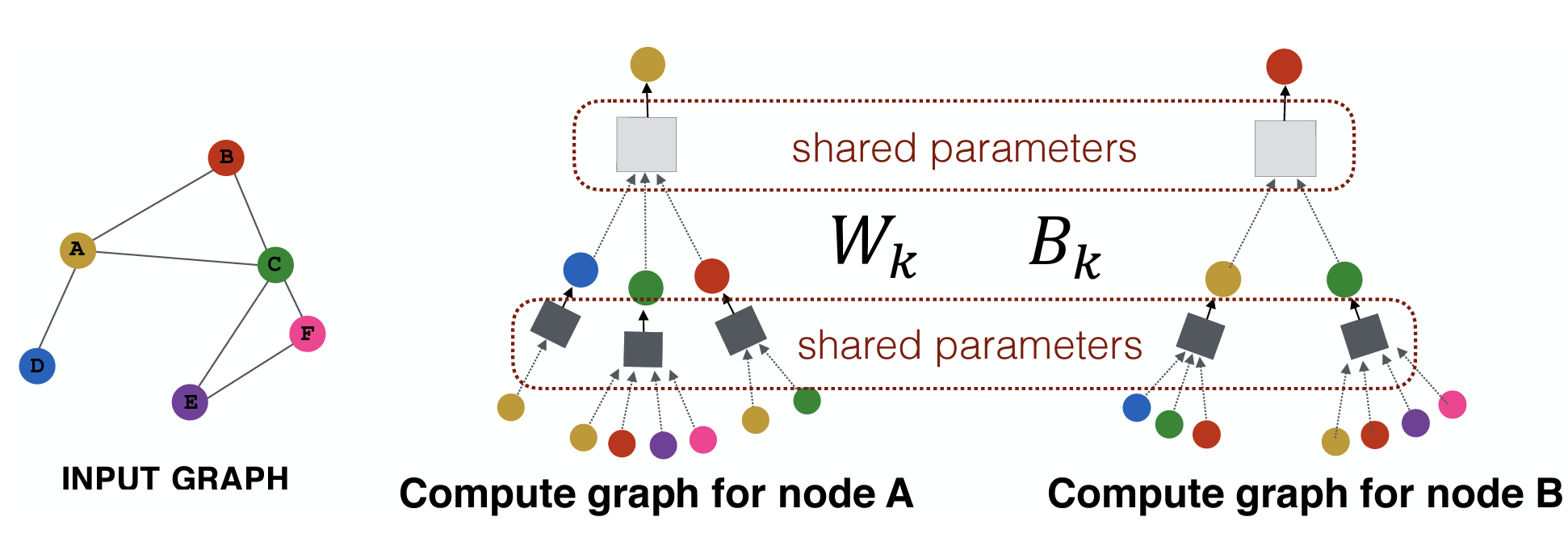
GNN Basics
Param sharing:参数共享
GNN beyond CNN/Transformers
- CNNs can be seen as a special GNN with fixed neighbor
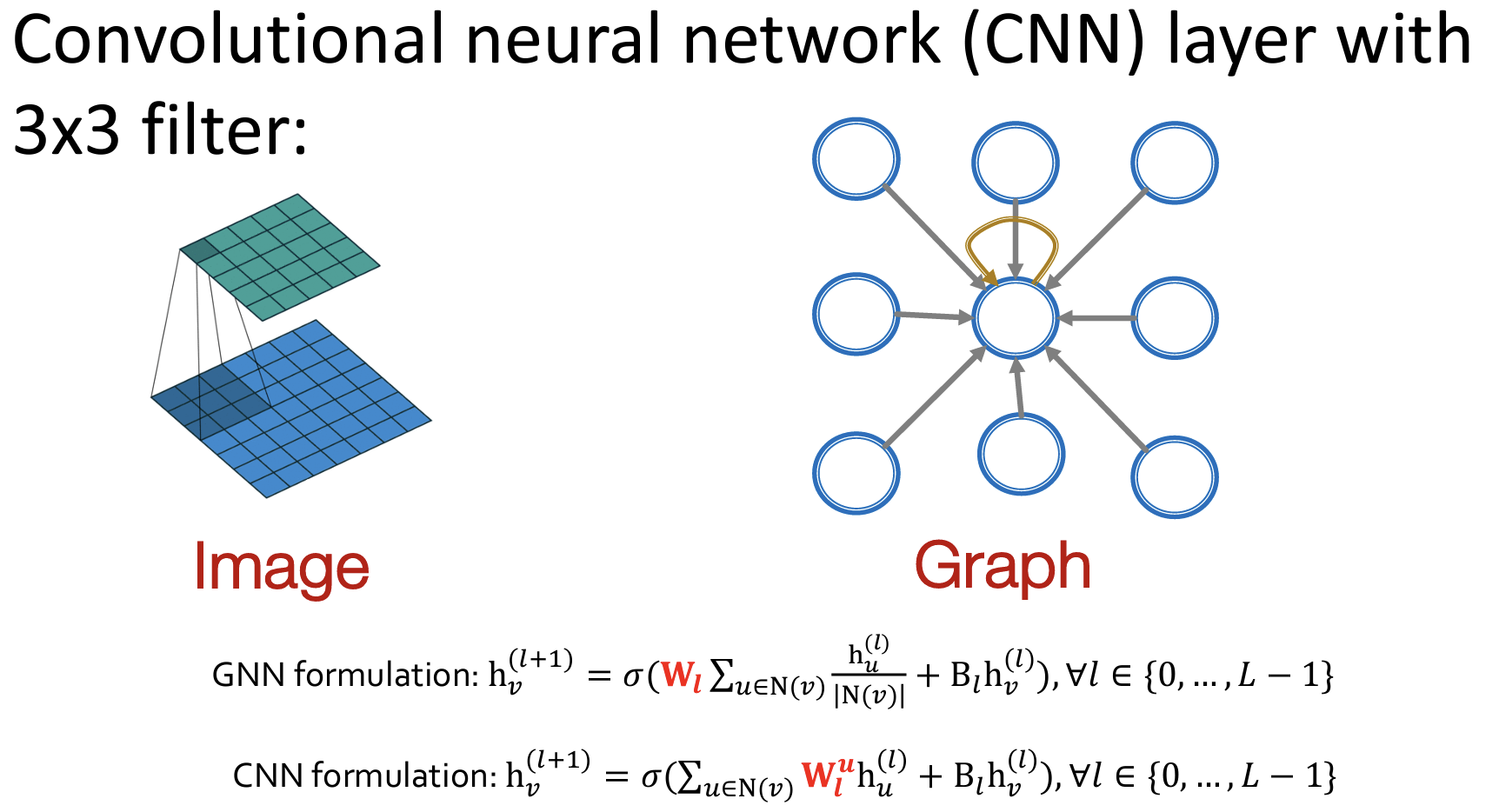
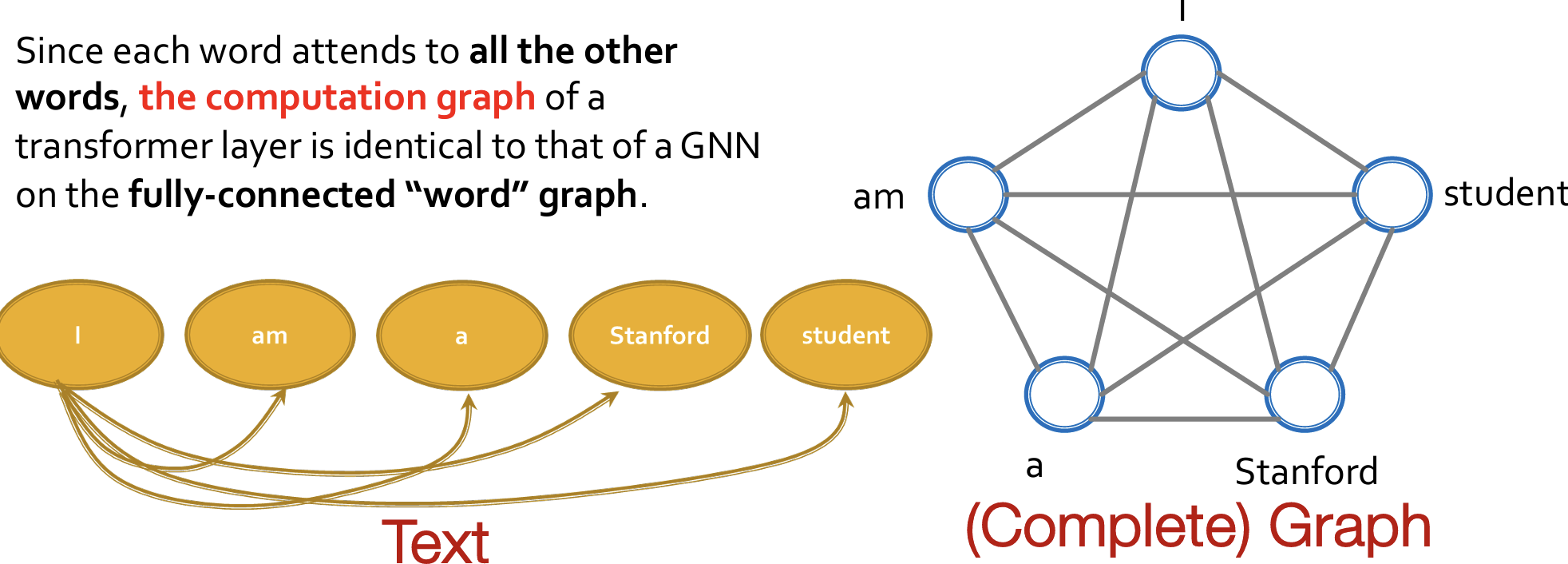
- Transformer layer can be seen as a special GNN that runs on a fullyconnected “word” graph!
Classic GNN
一个通用的GNN架构:
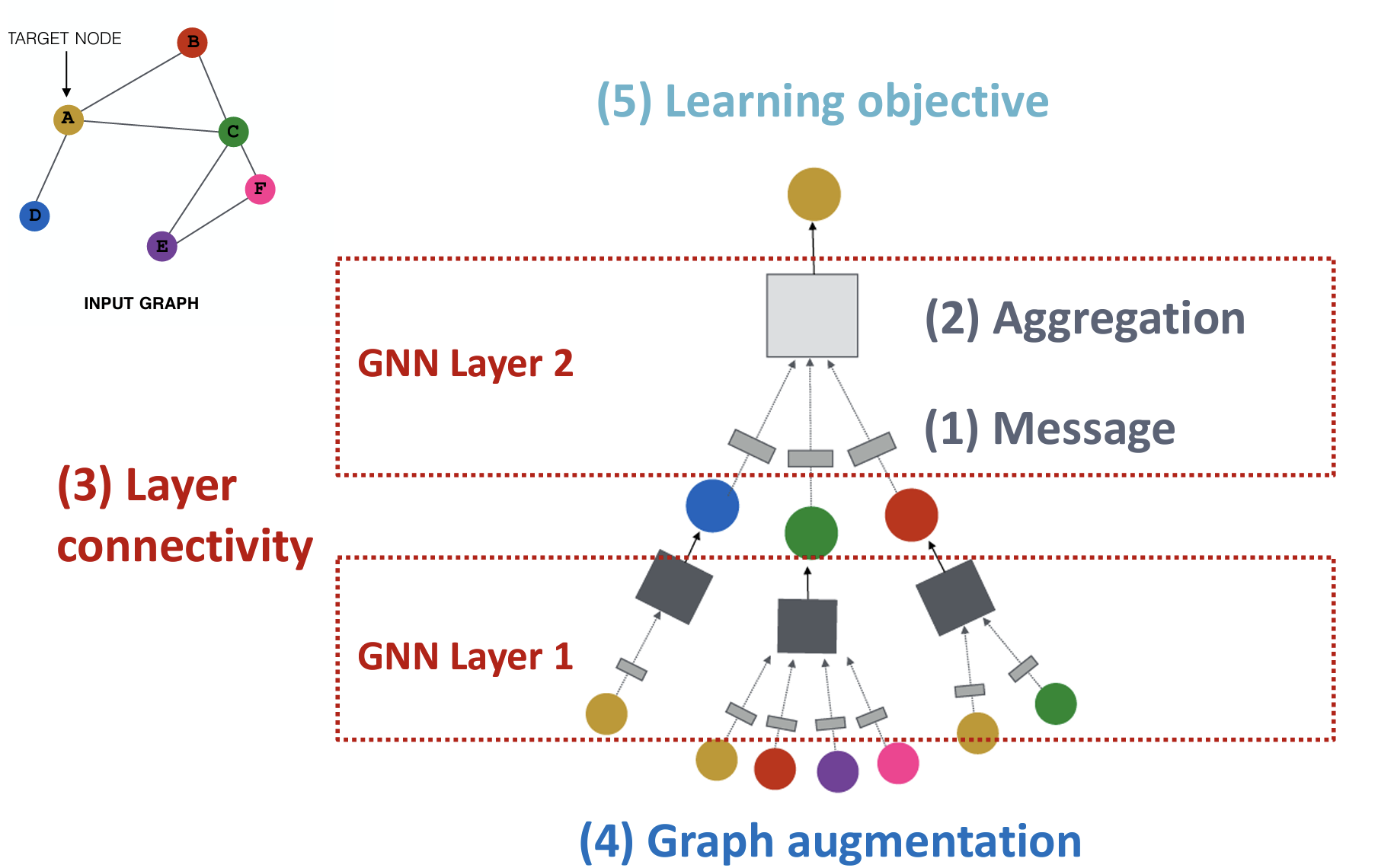
GNN Layer =(1) Message + (2)Aggregation
不同的策略 -> 不同的实例:GCN, GraphSAGE, GAT…..

Graph Convolutional Networks (GCN):
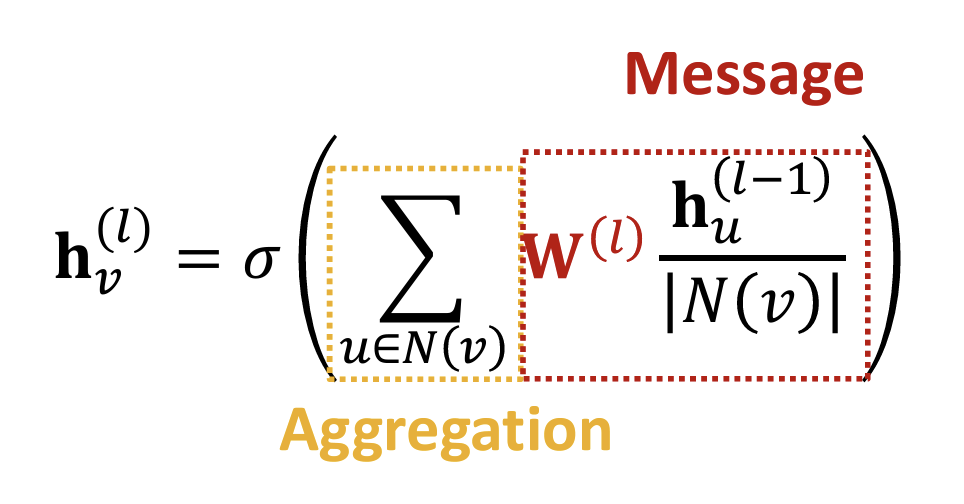
GraphSAGE:🔗
Transductive to Inductive
GCN直接对整个图进行卷积操作,每一层都需要遍历所有节点及其邻居节点。这种全图卷积的方式在处理大规模图时会遇到内存和计算瓶颈。
GraphSAGE提出了一种基于采样与聚合的策略,通过在训练过程中对节点的邻居进行采样,只选择部分邻居来计算节点的表示,从而大大减小了计算量和内存需求。主要解决了GCN在大规模图上应用的可扩展性问题。
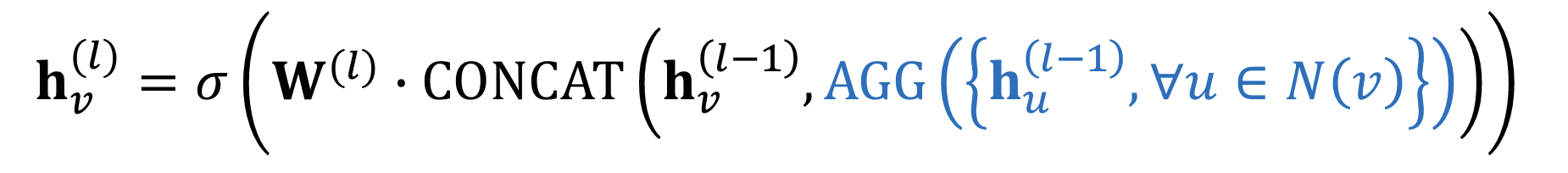
Graph Attention Networks(GAT):
Idea: Not all node’s neighbors are equally important;the NN should devote more computing power on that small but important part of the data. 【NN应该在数据中那个小而重要的部分上投入更多的计算能力。】
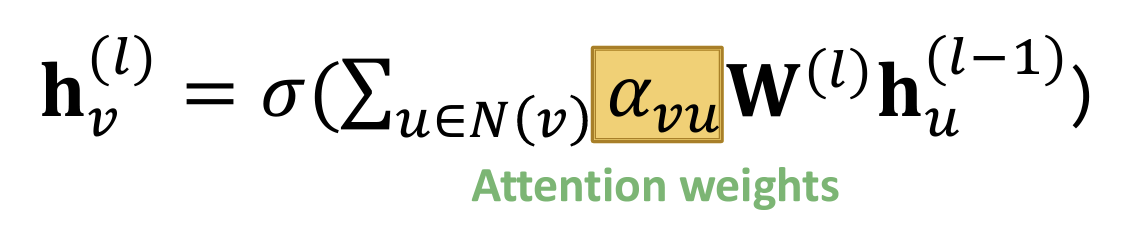
- Key benefit: Allows for (implicitly) specifying different importance values ($\alpha_{vu}$) to different neighbors
over-smoothing problem【过度平滑】:当stack的GNN层过多时,节点的感知域【Receptive field】可能过大甚至覆盖整个Graph,导致所有节点都感知整个图,使得所有节点趋于相同的embedding;
Key:the embedding of a node is determined by its receptive field
- 过多堆叠GNN Layer往往没用(不像CNN Layer那么有效),所以需要在GNN Layer较少(Shallow)的时候试图增强其感知能力
- 通过增强其message/Aggregation模块的NN的学习能力/通过前后concat线性层/通过添加 skip connection(集成学习视角)
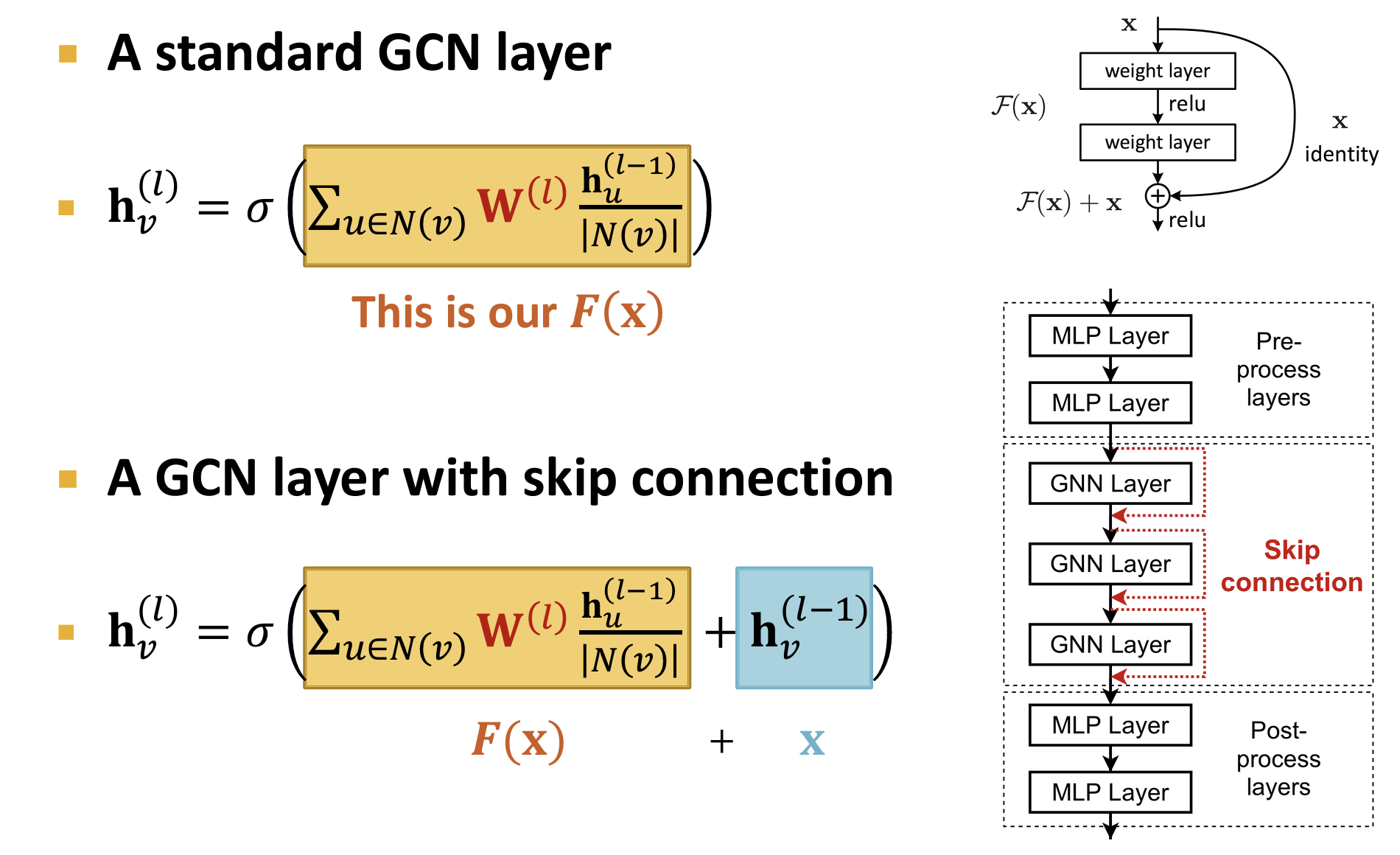
图增强/处理:应对稀疏图/稠密图/图过大等问题进行特征增强/图处理
- Graph Manipulation: Feature augmentation / Structure manipulation
- 后面的内容会cover这部分
Day3
主要内容:GNN

Graph Manipulation【图处理】
Graph Feature manipulation
- The input graph lacks features —— feature augmentation
Graph Structure manipulation
The graph is too sparse —— Add virtual nodes / edges
稀疏图:通常添加两跳虚边;例如在作者-文章的二部图中可以连接同一篇paper的coop的作者

The graph is too dense —— Sample neighbors when doing message passing
消息传递时随机采样而不使用所有的节点;和使用所有的子节点进行训练的期望一致,但是可以减少训练开销
The graph is too large —— Sample subgraphs to compute embeddings
unsupervised / self- supervised
我理解的这两个概念的区分:无监督更多的不设置标签例如clustering;自监督需要自己创建的标签;
- Node Level:使用节点的统计量作为标签进行训练, such as clustering coefficient, PageRank, …
- Edge Level:把一些edge进行遮蔽hide/mask进行作为标签进行训练
- Graph Level:图同构信息
评估指标
- 二分类模型的评估:混淆矩阵 / TPR==RecallRate / ROC(AUC)
- ROC曲线的xy坐标为两个rate:FPR以及TPR,性能越好的分类模型TPR>>FPR;如何绘制?对一个模型取不同的阈值分别计算FPR以及TPR坐标图中的一个点,形成曲线
图数据的划分
和其它的NN不相同,图数据集不是分离的数据点,所以需要特殊的数据划分(train/valid/test);这一部分的内容设计更加复杂的划分方法,在很多论文有所涉及,这里论述的只是最基础的划分方法。
Transductive Setting【直推】
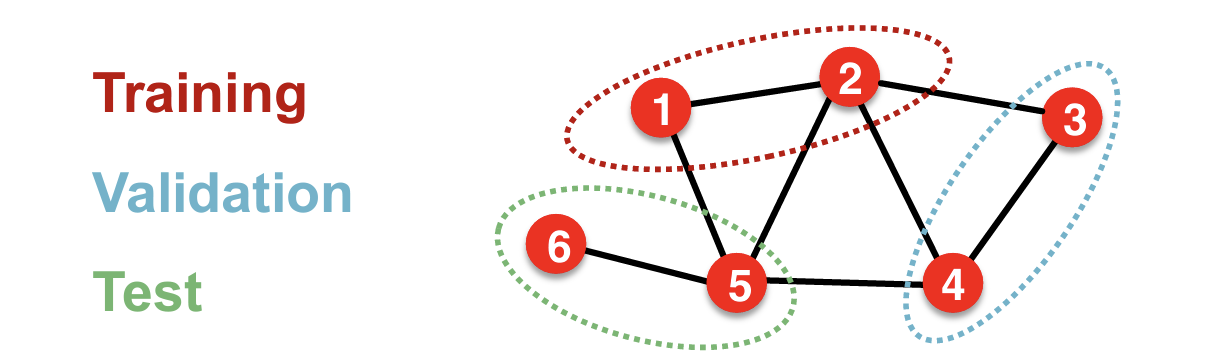
定义:在Transductive setting中,训练数据和测试数据的节点都属于同一个图。模型可以在训练时访问整个图的结构信息,包括测试节点及其连接,但不能访问测试节点的标签。
特点:
- 同一个图:训练和测试都在同一个图上进行,测试节点在训练时是已知的。
- 全局信息:模型可以利用整个图的结构信息来进行学习,这包括训练节点和测试节点之间的连接。
- 目标:学习节点的嵌入或特征,使得在测试节点上的分类或回归任务表现良好。【Only applicable to node / edge prediction tasks】无法在Graph-Level分类相关的任务使用。
Inductive Setting【归纳】
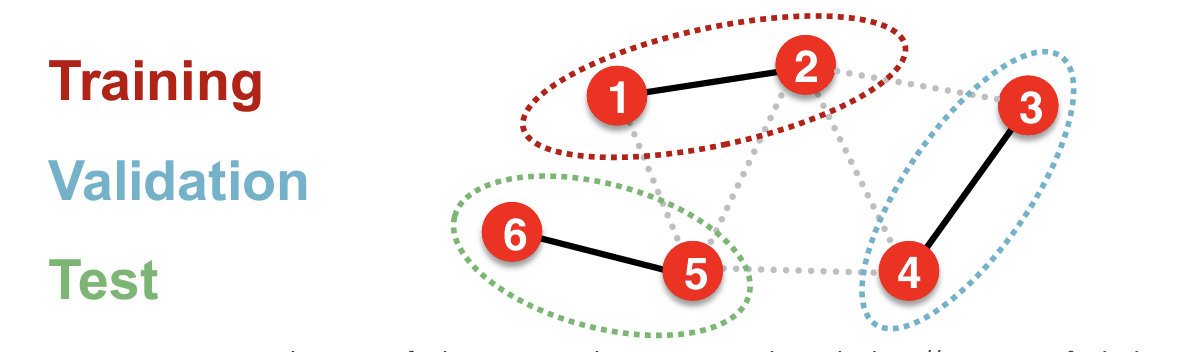
定义:在Inductive setting中,训练数据和测试数据的节点属于不同的图。模型在训练时只能访问训练图的结构和标签信息,测试时模型需要在完全未知的图或新节点上进行预测。
特点:
- 不同的图:训练和测试在不同的图上进行,或者在同一个图上但测试节点在训练时是未知的。
- 局部信息:模型不能利用测试图的结构信息进行训练,只能基于训练图进行学习。
- 目标:在新的图或新节点上泛化良好,即使这些图或节点在训练时不可见。【Applicable to node / edge / graph tasks】
具体示例:Transductive link prediction split:分为四类边【训练用信息边、训练用监督边、验证用边、测试用边】
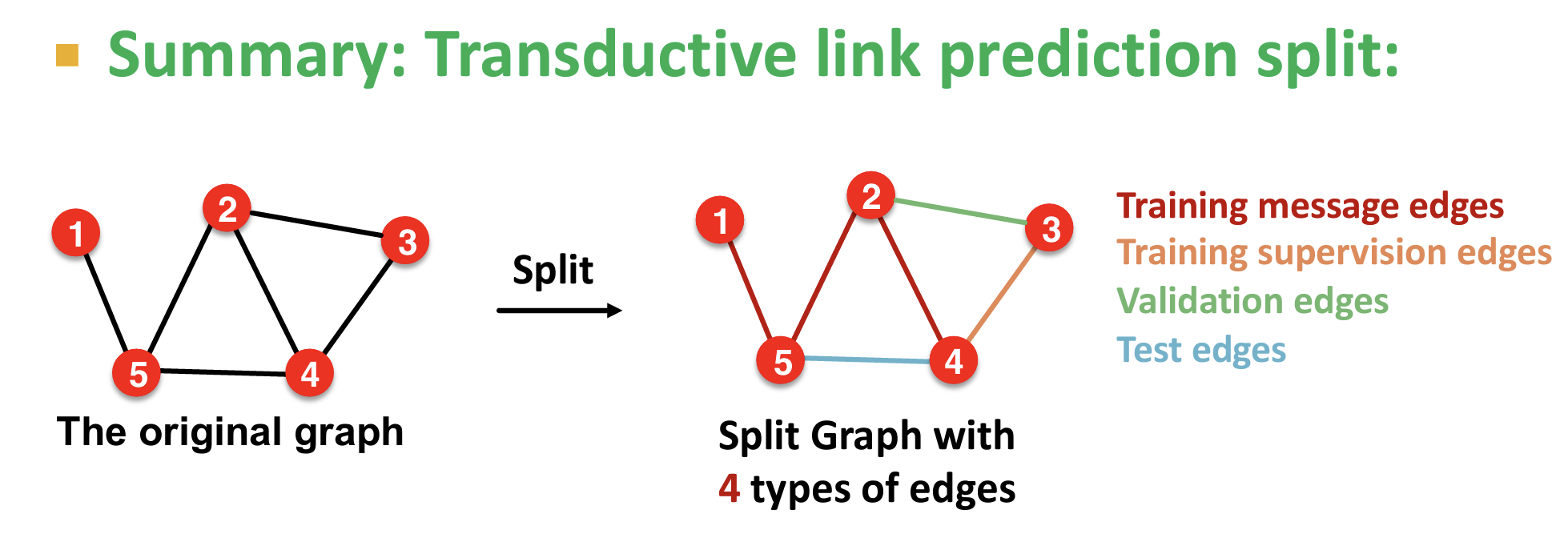
The Power of GNN
- 对每个节点的计算可以构建一个计算图【Computational Graph】,对应一颗以该节点为根的子树;在该结构的aggragation聚合层为单射时其表达能力最强【单射可以区分不同的结构】
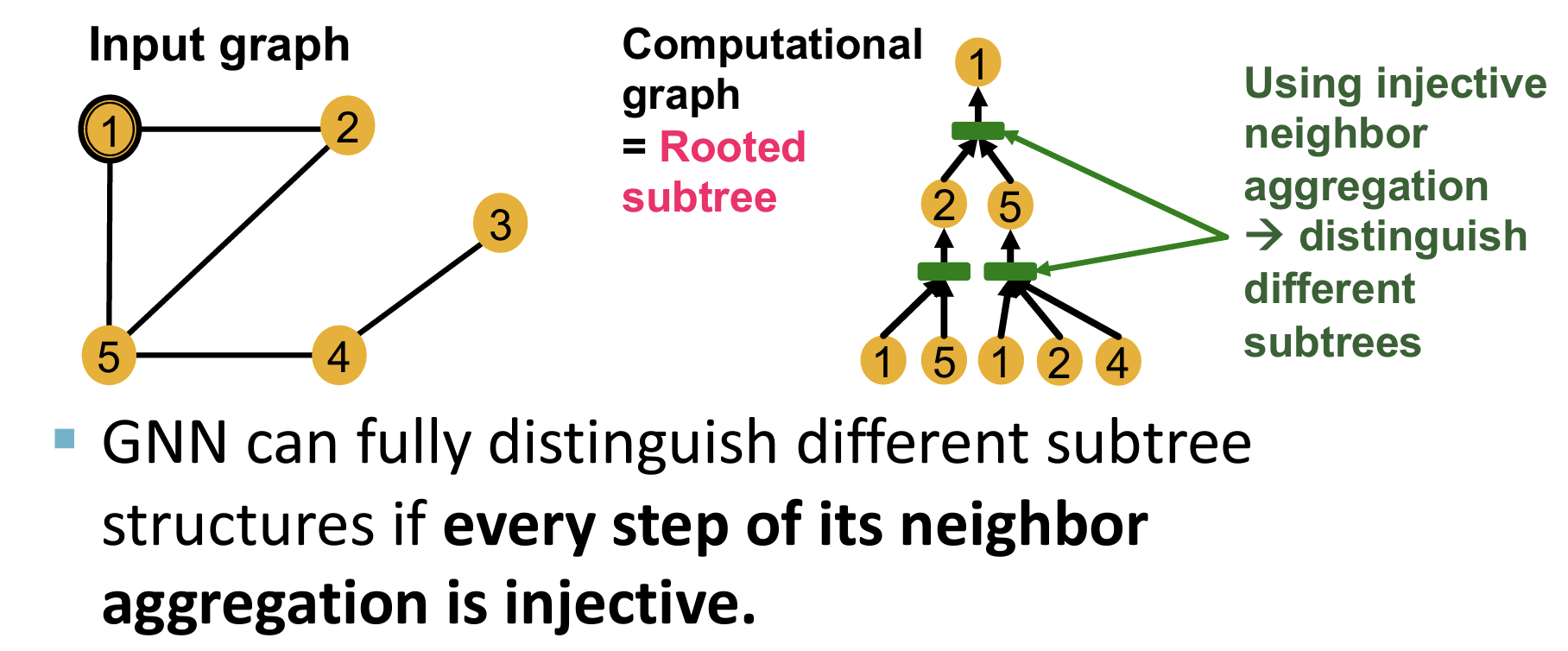
Key observation: **Expressive power of GNNs can be characterized by that of neighbor aggregation functions they use.**【GNNs 的表达能力可以用其使用的 neighbor aggregation functions 所表征】
e.g. failure 案例研究:
- GCN:使用平均池化
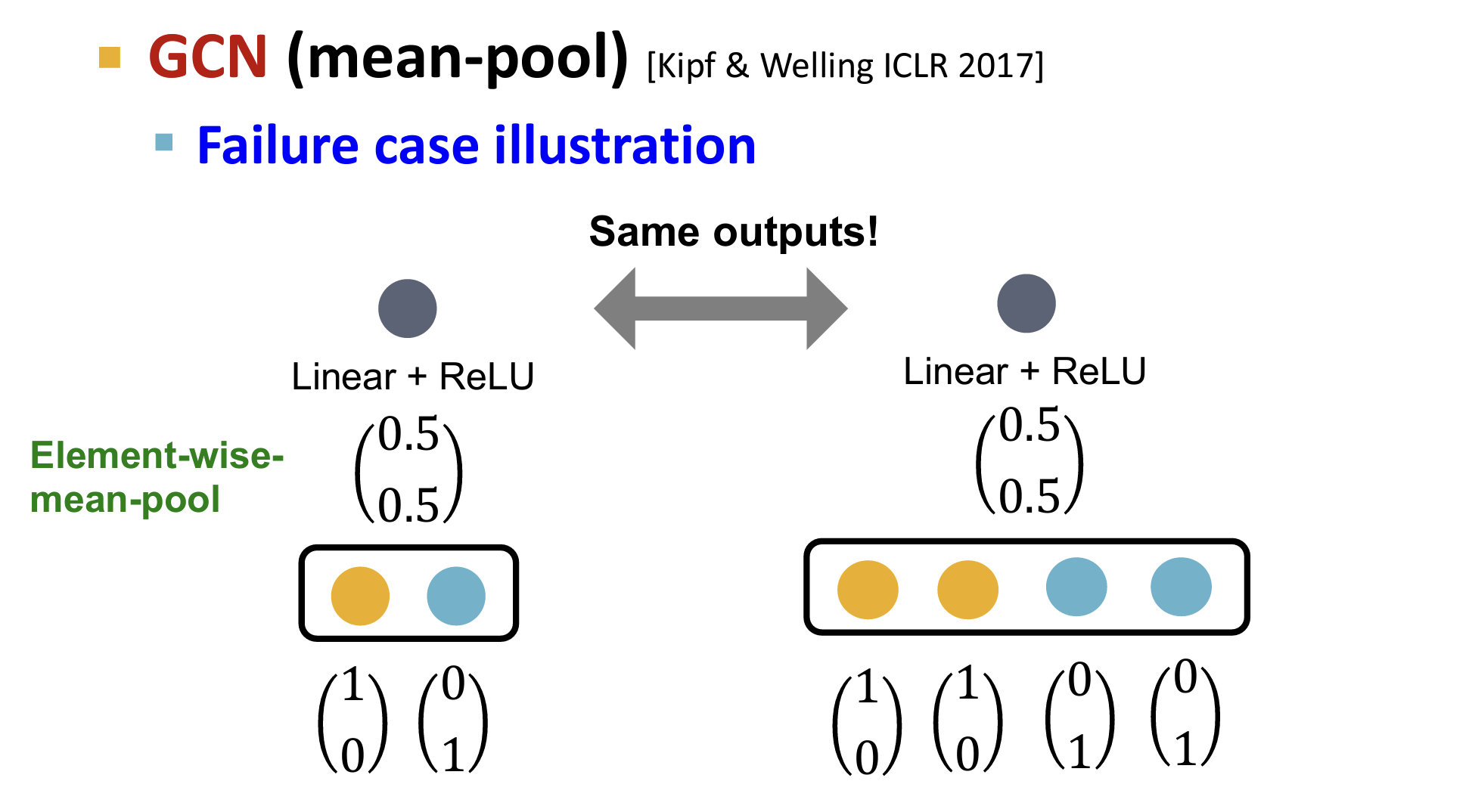
- GraphSAGE:使用最大池化
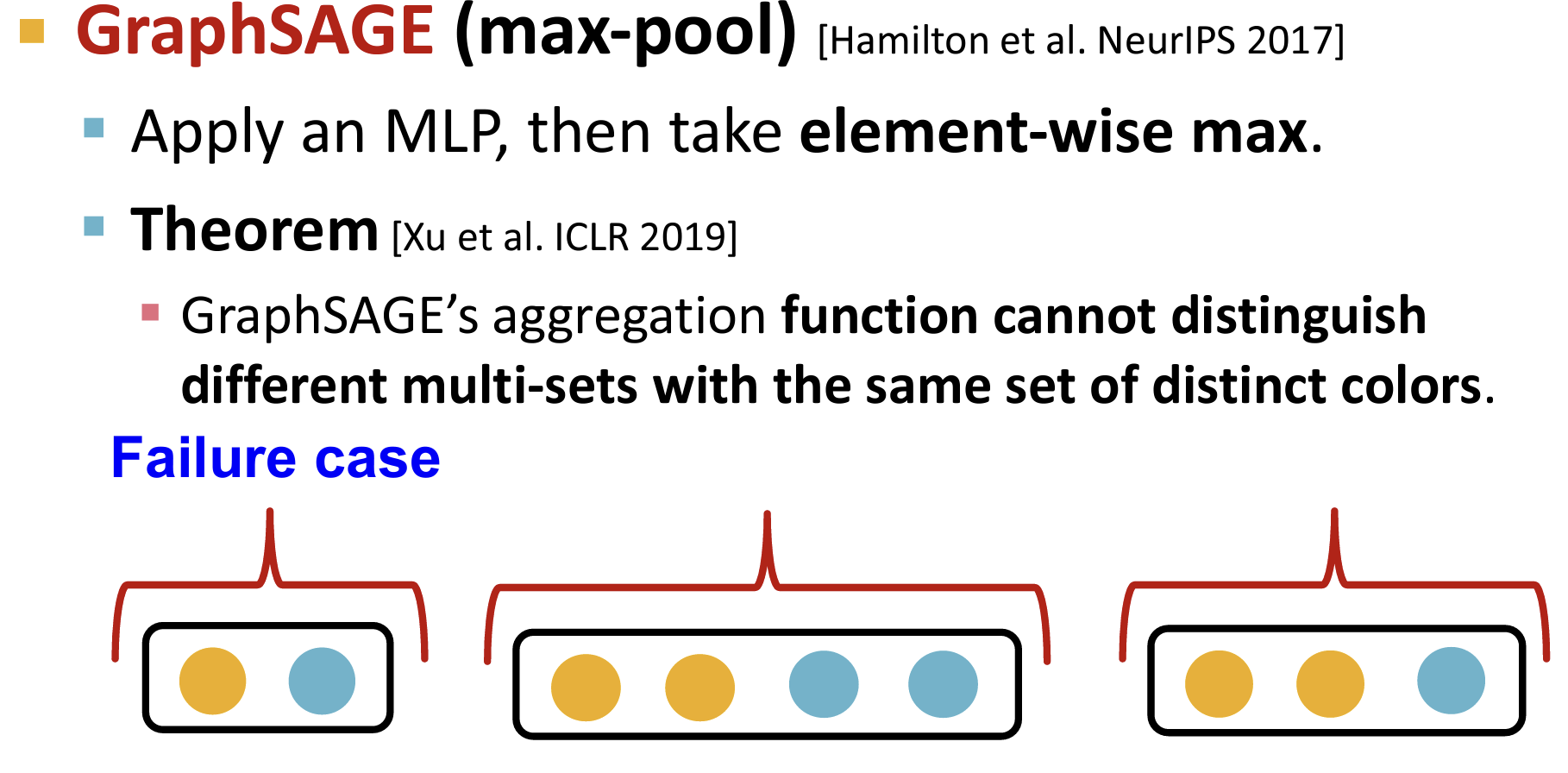
如上案例所示,GCN and GraphSAGE’s aggregation functions fail to distinguish some basic multi-sets【可重复元素集合】; hence not injective.【因此非most powerful】
THE most expressive GNN in the class of message-passing GNNs:Graph Isomorphism Network (GIN)
GIN‘s neighbor aggregation function is injective.

Day3-Lab
在Colab 2中,将使用PyTorch Geometric (PyG) 构建自己的图神经网络,并将该模型应用于两个Open Graph Benchmark (OGB)数据集。这两个数据集将用于基准测试你的模型在两个不同图任务上的性能:1)节点属性预测,预测单个节点的属性;2)图属性预测,预测整个图或子图的属性。
实现一个简单的GCN用于节点预测
1 | class GCN(torch.nn.Module): |
Day4

Heterogenous graphs[异质图]
- 异质图(Heterogeneous Graph)是指由不同类型的节点和边构成的图结构(a graph with multiple relation types)。 在异质图中,节点和边可以具有多样化的属性和关系,代表了不同实体以及它们之间的复杂关联。
- 定义:

现实问题的Graph大多是异质图
可以将异质图中的节点/边的类型编码为节点/边的特征(例如one-hot)使得其变为标准图
How To Solve?
关系图卷积网络(Relational Graph Convolutional Network, R-GCN)
是一种扩展了传统图卷积网络(GCN)的模型,专门用于处理异质图中的多种关系。R-GCN通过在图卷积操作中引入关系类型来捕捉不同类型节点和边之间的复杂关系。这使得R-GCN在处理包含多种关系的复杂图数据时更加有效。
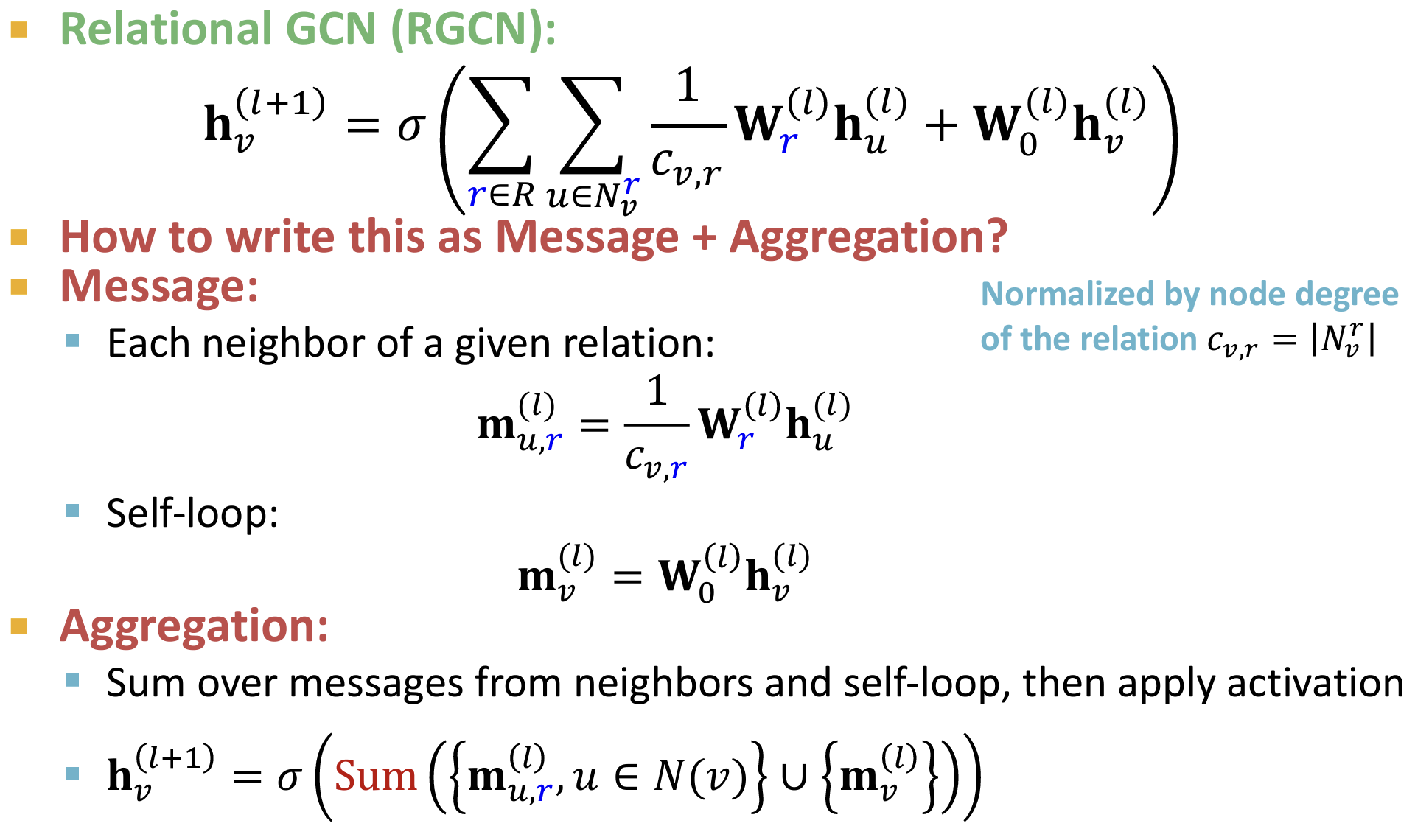
- R-GCN存在问题?参数过多:
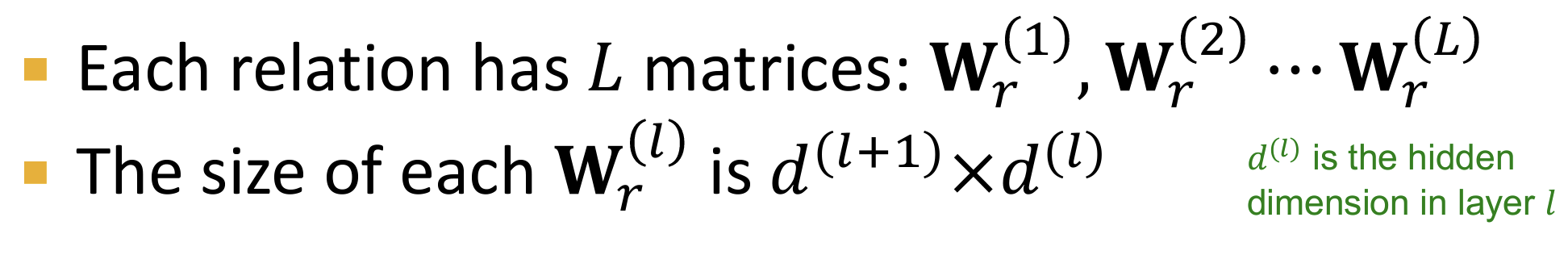
每一层的每一种relation类型都对应一个权重$\mathbf{W}_r^{(l)}$,如果关系类型过多,模型参数量会非常大,容易导致过拟合。
为了防止过拟合,常用的两种正则化方法是使用块对角矩阵Block Diagonal Matrices和基/字典学习:
使用块对角矩阵:这种方法通过强制权重矩阵 $\mathbf{W}_r^{(l)}$ 具有块对角结构,从而减少参数数量。具体来说,块对角矩阵将权重矩阵分成若干个较小的子矩阵(块),并使得这些子矩阵之间没有相互影响。
关键思想:稀疏化权重矩阵

基/字典学习(Basis/Dictionary Learning):每种关系类型的权重矩阵$\mathbf{W}_r^{(l)}$由若干基权重矩阵的线性组合表示。具体来说,定义一组基权重矩阵${ \mathbf{B}_1, \mathbf{B}_2, \ldots, \mathbf{B}_K }$,然后通过关系特定的系数组合这些基权重矩阵来构造每个关系类型的权重矩阵。
关键思想:使不同的权重矩阵共享参数

GNN vs Heterogenous GNN
两者的区别?
Message:消息传递阶段,H-GNN对关系类型建模,不同的关系类型具有不同的linear权重


Aggregation:聚合阶段,H-GNN同样对关系类型进行建模,使用两阶段的聚合方法:先对同种关系类型的消息进行聚合,然后进行总的聚合(例如concat)


Prediction:在预测阶段,需要考虑不同的关系类型

Day5
Knowledge Graphs

关系模式
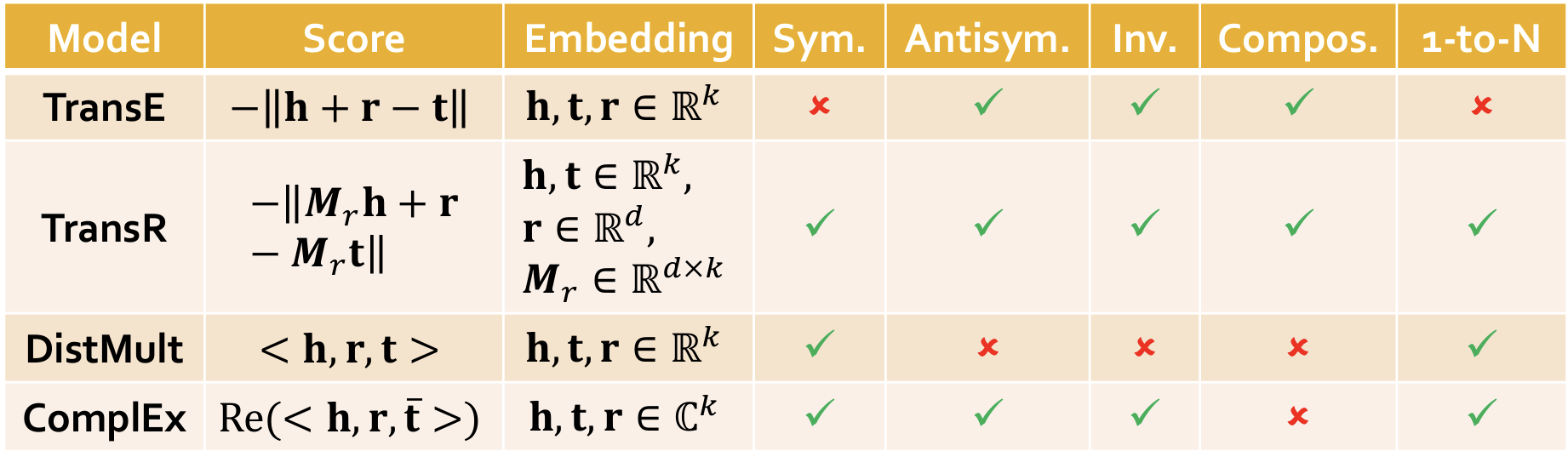
对称关系(Symmetric Relations)
定义:如果关系 ( r(h, t) ) 成立,那么 ( r(t, h) ) 也成立。
符号表示:$$ r(h, t) \Rightarrow r(t, h) \forall h, t $$
示例:
- 家人(Family):如果Alice是Bob的家人,那么Bob也是Alice的家人。
- 室友(Roommate):如果Alice是Bob的室友,那么Bob也是Alice的室友。
反对称关系(Antisymmetric Relations)
定义:如果关系 ( r(h, t) ) 成立,那么 ( r(t, h) ) 不成立。
符号表示:$$ r(h, t) \Rightarrow \neg r(t, h) \forall h, t $$
示例:
- 上位词(Hypernym):一个词具有更广泛的意义。例如,“狗(dog)”是“贵宾犬(poodle)”的上位词,但反之不成立。
逆关系(Inverse Relations)
定义:如果关系 ( r(h, t) ) 成立,那么存在一个逆关系 ( r’(t, h) ) 也成立。
符号表示:$$ r(h, t) \Rightarrow r’(t, h) $$
示例:
- 导师与学生(Advisor and Advisee):如果Dr. Smith是John的导师,那么John是Dr. Smith的学生。
传递关系(Composition/Transitive Relations)
定义:如果 ( r(x, y) ) 和 ( r(y, z) ) 都成立,那么 ( r(x, z) ) 也成立。
符号表示:$$ r(x, y) \land r(y, z) \Rightarrow r(x, z) \forall x, y, z $$
示例:
- 家庭关系:我母亲的丈夫是我的父亲。如果Alice是Bob的母亲,Bob是Charlie的丈夫,那么Alice是Charlie的母亲。
一对多关系(1-to-N Relations)
定义:一个实体可以与多个实体通过相同关系相关联。
符号表示:$$ r(h, t_1) , r(h, t_2), \ldots , r(h, t_n) $$ 都成立。
示例:
- 学生关系(StudentsOf):一个教师有多个学生。例如,教师Dr. Smith有学生John、Emily、Sarah。
KG Completion
KG的补全:例如Is link (h,r,t) in the KG?
Introduce TransE / TransR / DistMult / ComplEx models【四种知识图谱嵌入的方法】 with different embedding space and expressiveness
KG Reasoning
- 知识图谱具体的推理任务需要根据一系列的query来表述,也就是说在给定的不完整并且大规模的知识图谱中对输入的自然语言形式的query进行推理并返回结果,而query可以分为One-hop Queries,Path Queries和Conjunctive Queries三种,分别是单次跳转的推理、多次跳转的推理、联合推理,可以用下面的图来表示三种query之间的关系:

可以使用知识图谱嵌入:考虑将知识图谱上的问答转化到向量空间中进行,而具体的方法就是将query也转换成一个向量,并使用嵌入模型的打分函数来评估结果。一个查询在向量空间中可以表示为:

Query2Box
论文🔗:QUERY2BOX: REASONING OVER KNOWLEDGE GRAPHS IN VECTOR SPACE USING BOX EMBEDDINGS
- 问题:在处理联合推理时每个节点都代表多个entity,如何在隐空间定义其交叉操作?
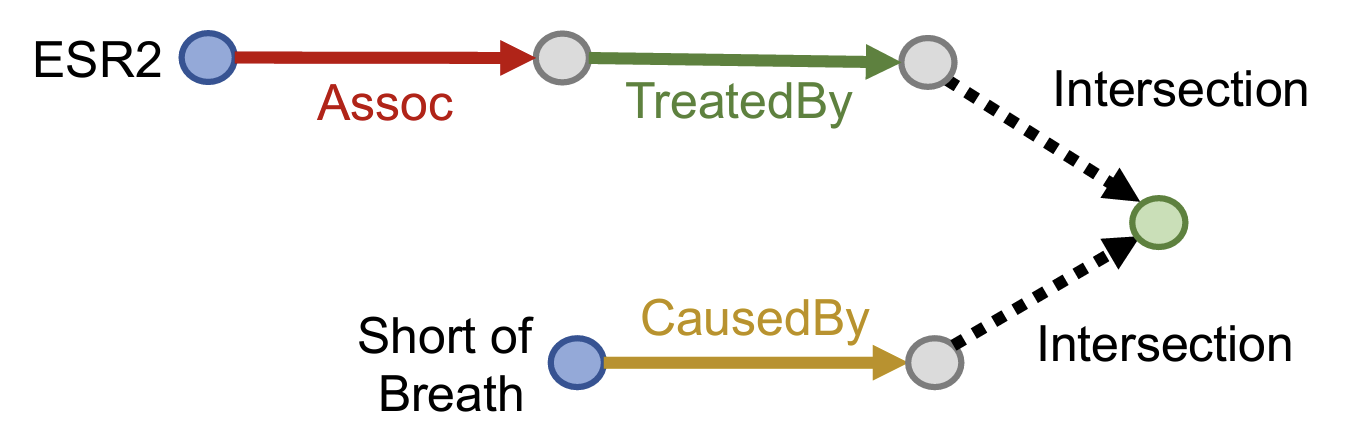
- 核心思想:Embed queries with hyper-rectangles (boxes)【将查询嵌入为超矩形即box】
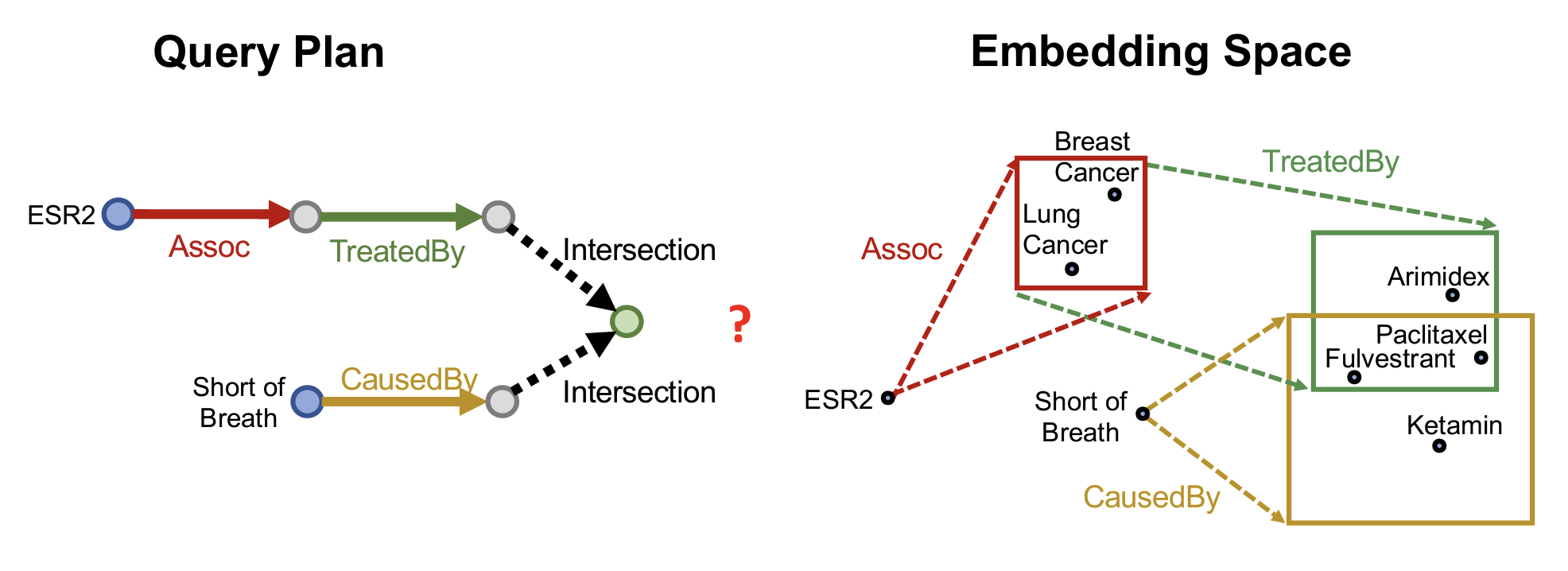
- 如何定义多个Box的交集【intersection】操作?

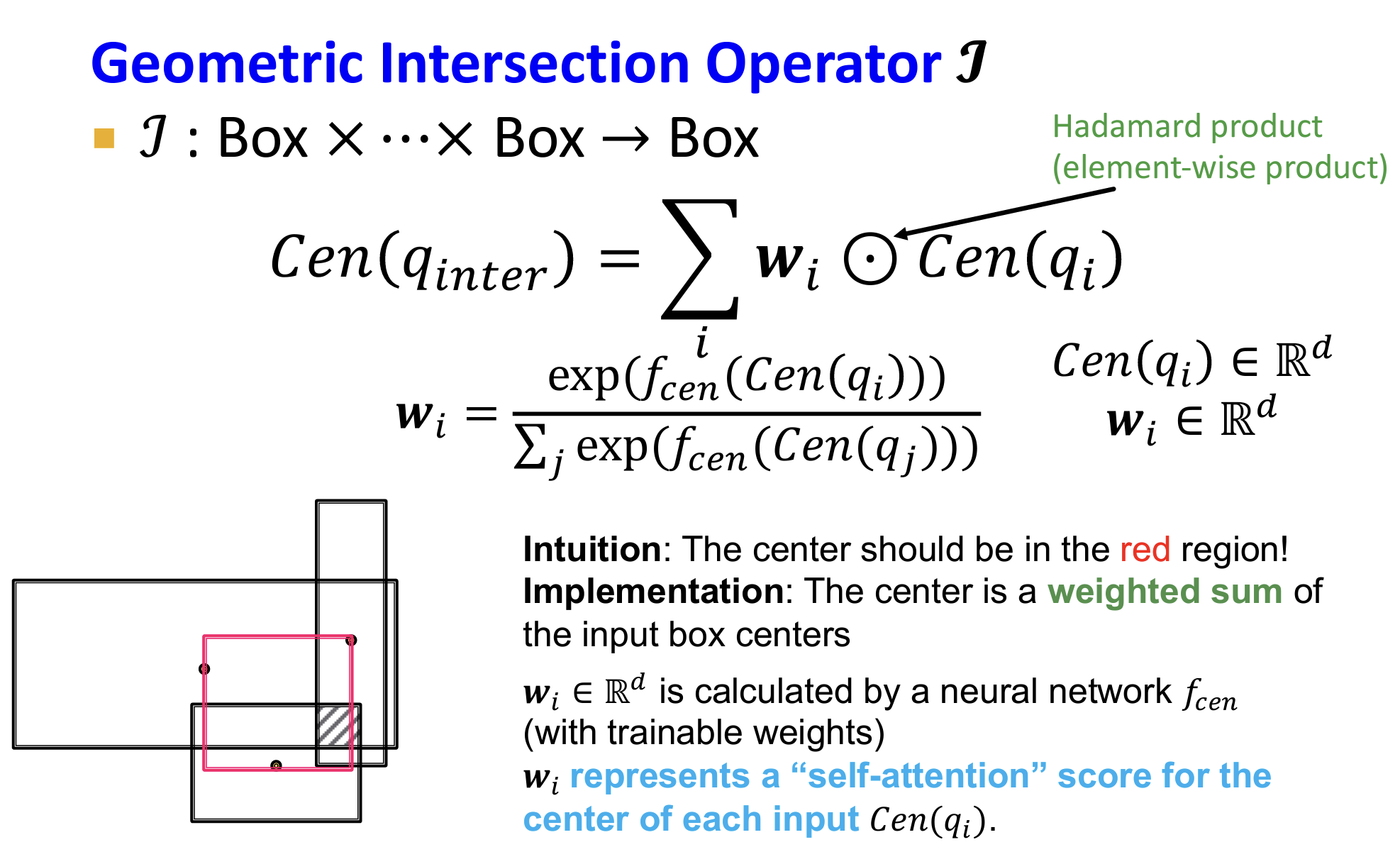
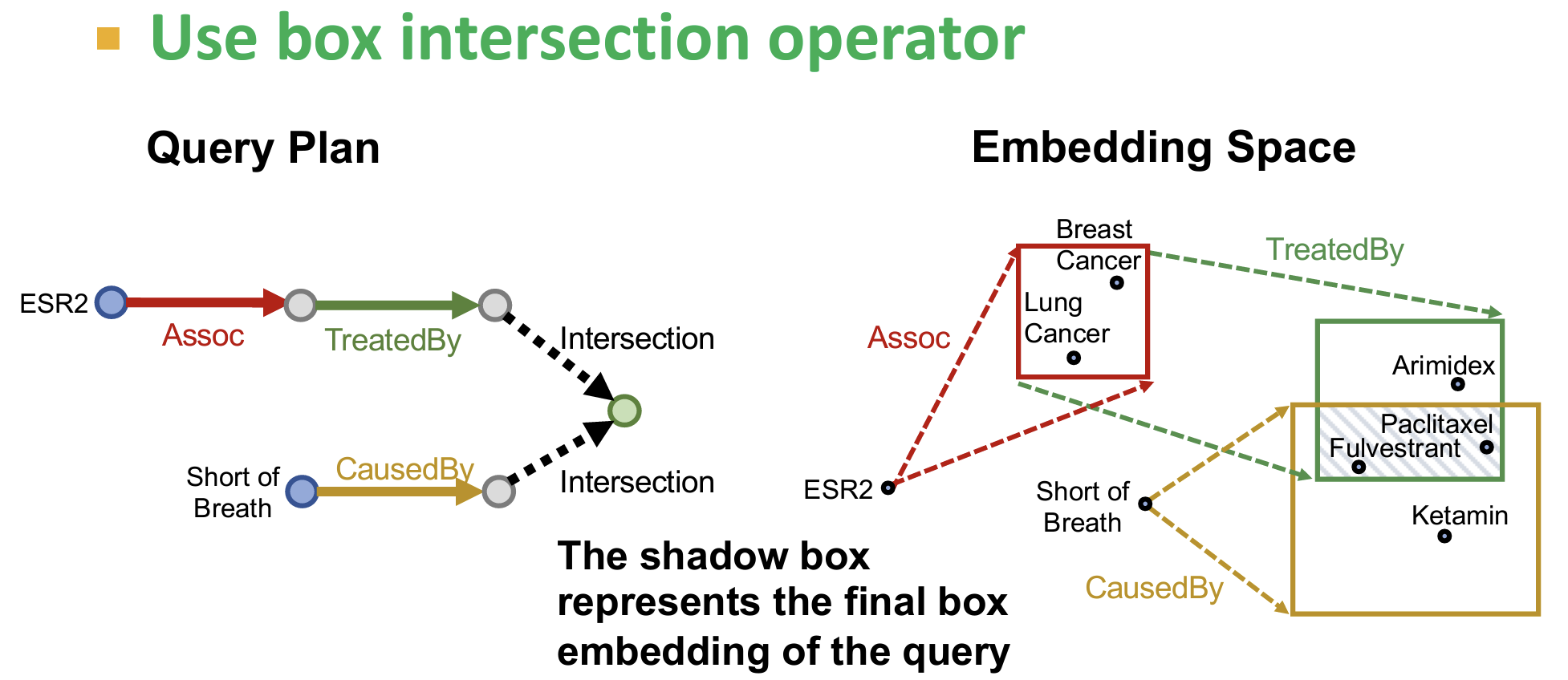
- 对于Union操作的扩展
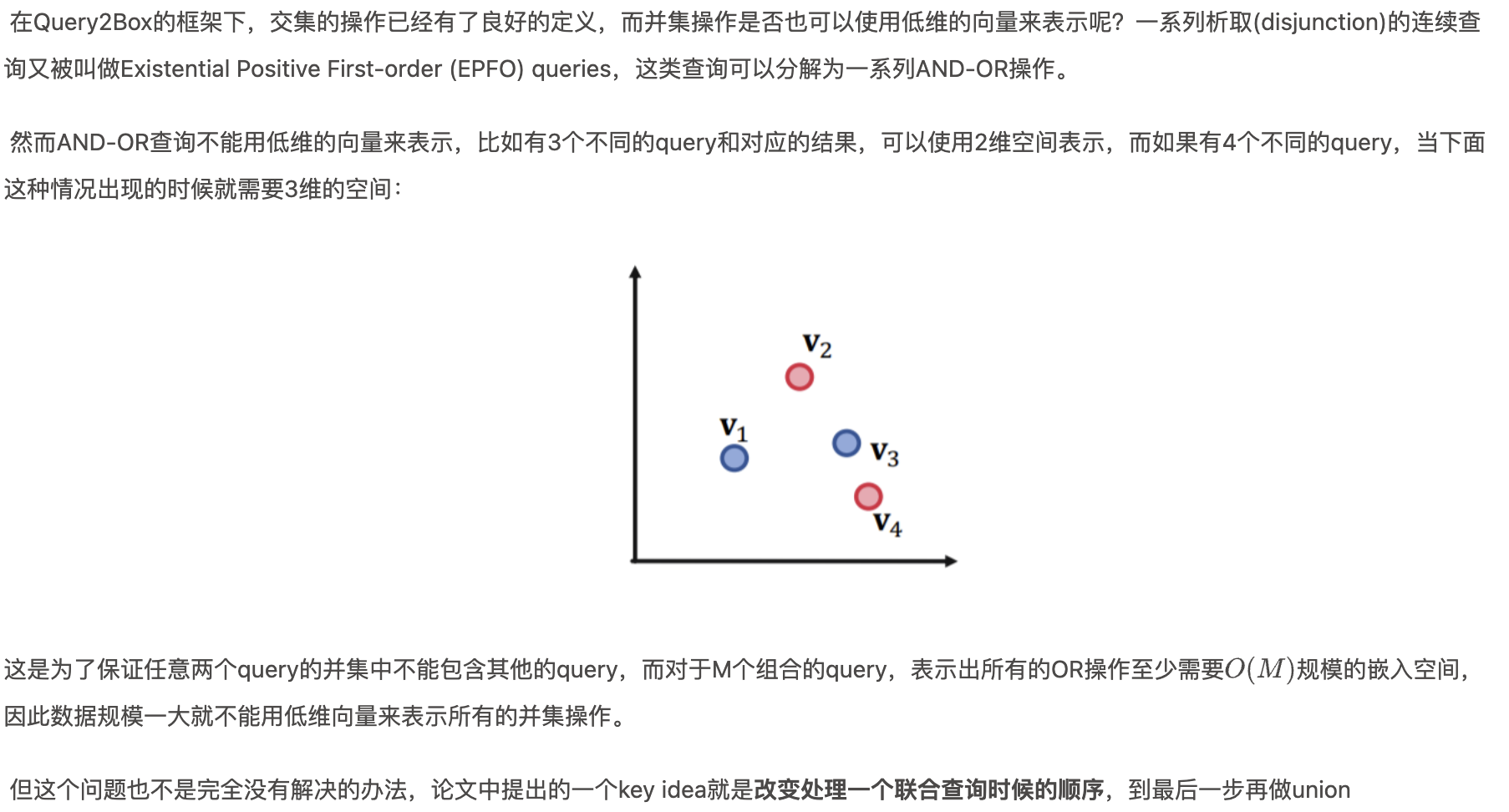
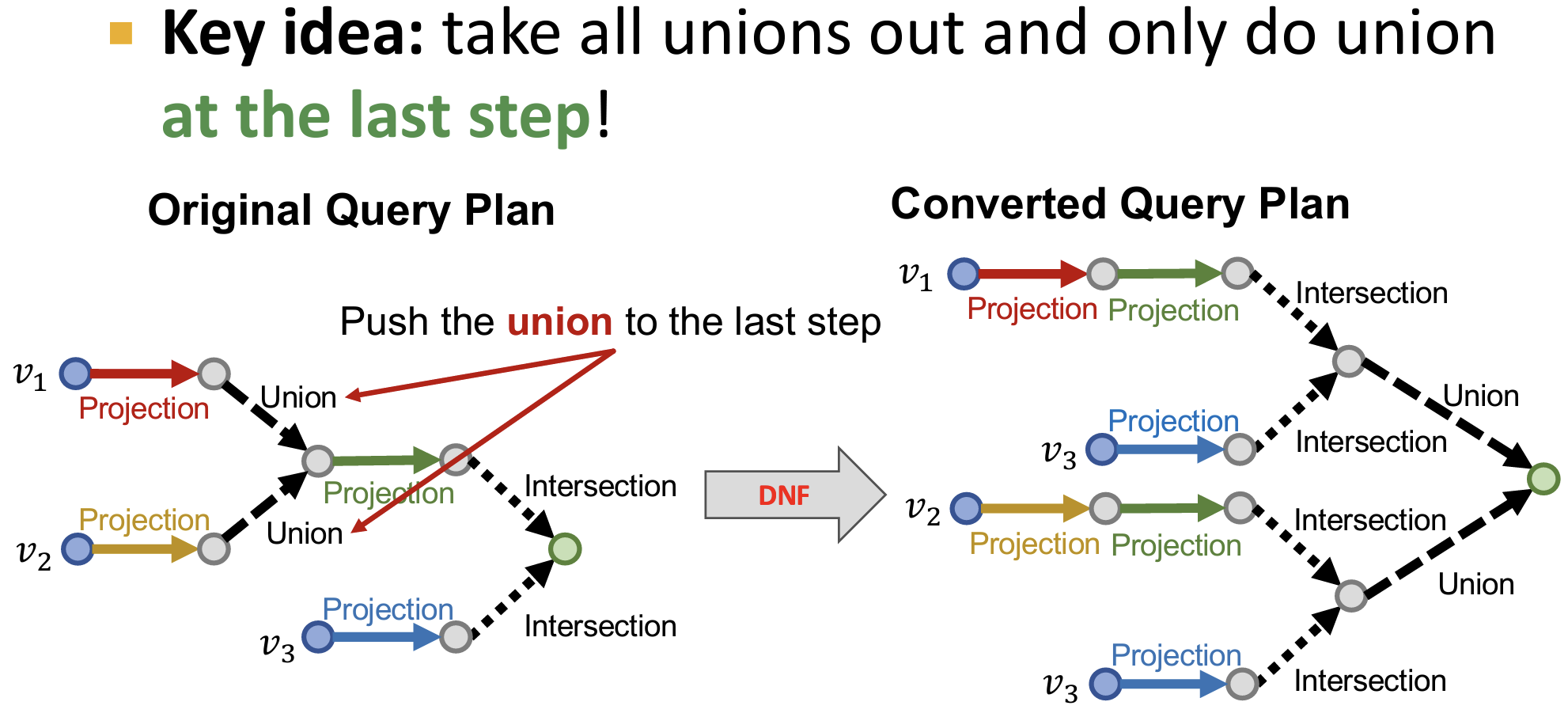
Query2Box的训练
- 在Query2Box模型中,需要训练的参数主要有所有的实体的嵌入向量,所有的关系的嵌入向量和Intersection运算中的各种参数。
- 一个很直观的想法是,在训练Qeury2Box模型的过程中,对于一个查询q的嵌入向量,我们要让属于q中的实体v对应的打分函数最大化,而要让不在其中的打分函数最小化,为此需要用到负采样,也就是在训练的过程中,对于每个正样本v随机选取一个负样本与之对应,具体的训练过程可以分为以下几个步骤:

- 在训练之前我们需要提取出一系列查询,而这个过程称为Query Generation,可以通过一系列模板生成:
Day6
Fast neural subgraph matching and Counting

子图
图的组成结构,可以区分和描述一个图
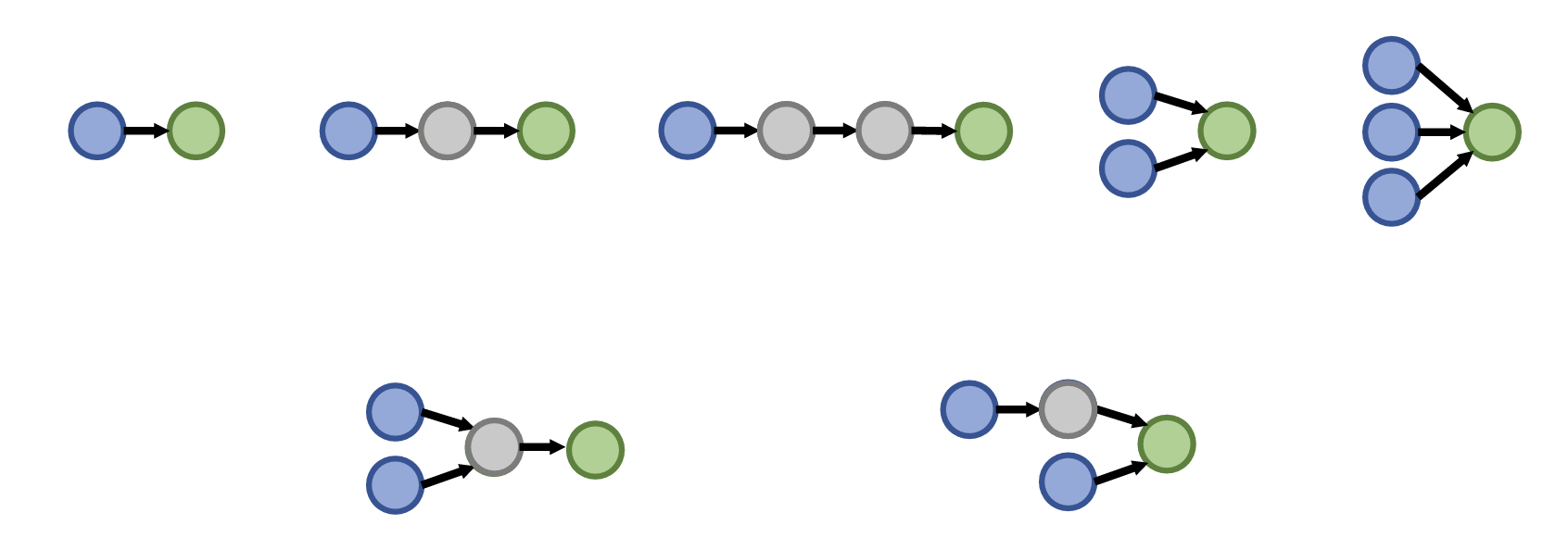
两种定义方法:
Node-induced subgraph:节点诱导子图

Edge-induced subgraph:边诱导子图

两种方法生成的子图都有其应用范围:例如化学结构适合节点诱导,而知识图谱适合边诱导(因为知识图谱focus on边表示的逻辑关系)
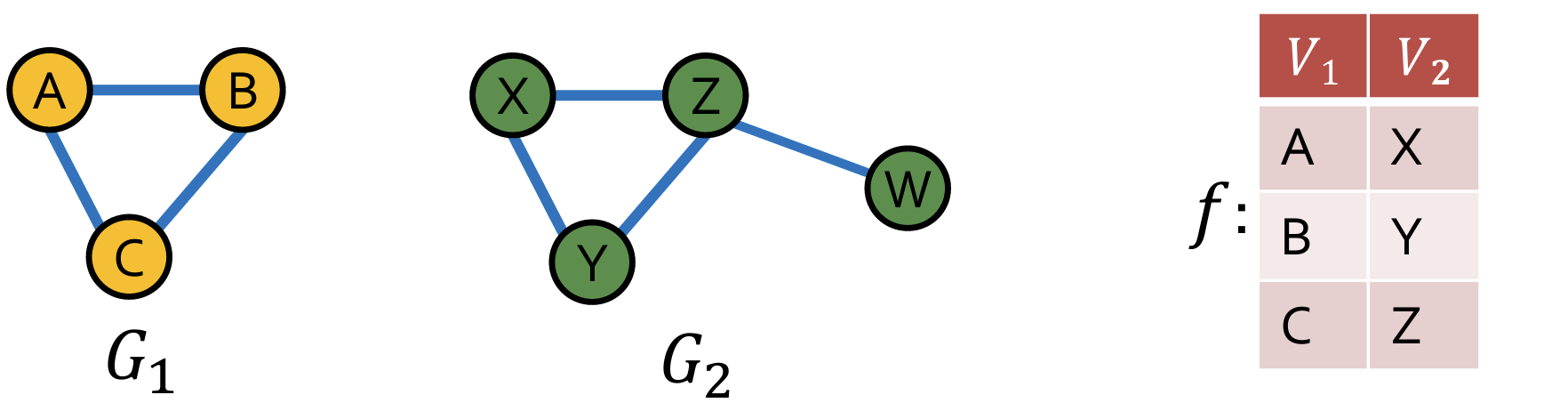
Graph Isomorphism 图同构
- 定义:core idea 双射 bijection
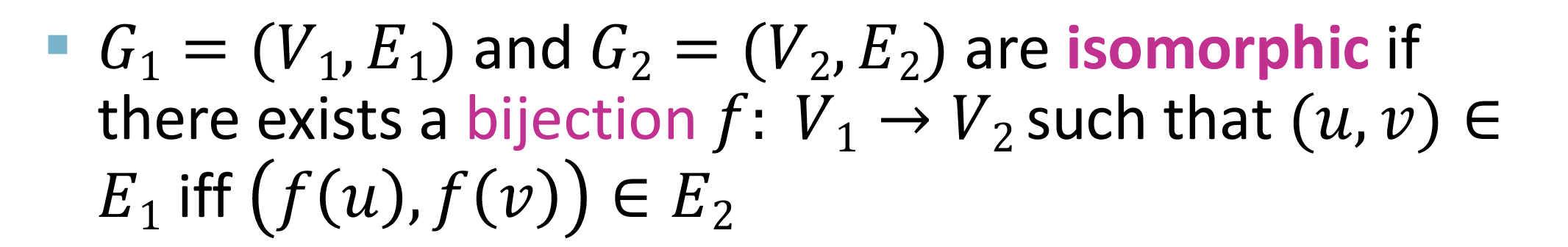
- 图同构的判断问题是NP-hard
- 引申:子图同构问题:图G1 和 图G2的子图 同构:
Network motifs 网络图案
定义:recurring, significant patterns of interconnections 在网络中反复出现的、具有显著意义的连接模式。
特点特性:
- Pattern: Small (node-induced) Subgraph 较小的节点诱导子图,节点诱导必须满足所有诱导节点之间的边都一致
- Recurring: Found Many Times, i.e., with High Frequency 重复出现:多次被发现,即具有高频率
- 定义:一个模式在网络中被认为是motif,如果它在网络中多次出现,其出现频率明显高于偶然情况。
- 如何定义频率:通过在网络中计算特定模式的出现次数来定义频率。
- Significant: More Frequent Than Expected, i.e., in Randomly Generated Graphs显著性:出现频率高于预期,即在随机生成的图中
如何判断motifs?使用相同的图统计指标生成随机图,利用统计指标(例如z分数:对所有的待评估图案作为一个向量,计算z分数后归一化)评估 motif 的显著性。

Neural Subgraph Match
- 如何基于神经网络(GNN)进行子图匹配(which is np-hard)
方法:使用Order Embedding 有序嵌入空间
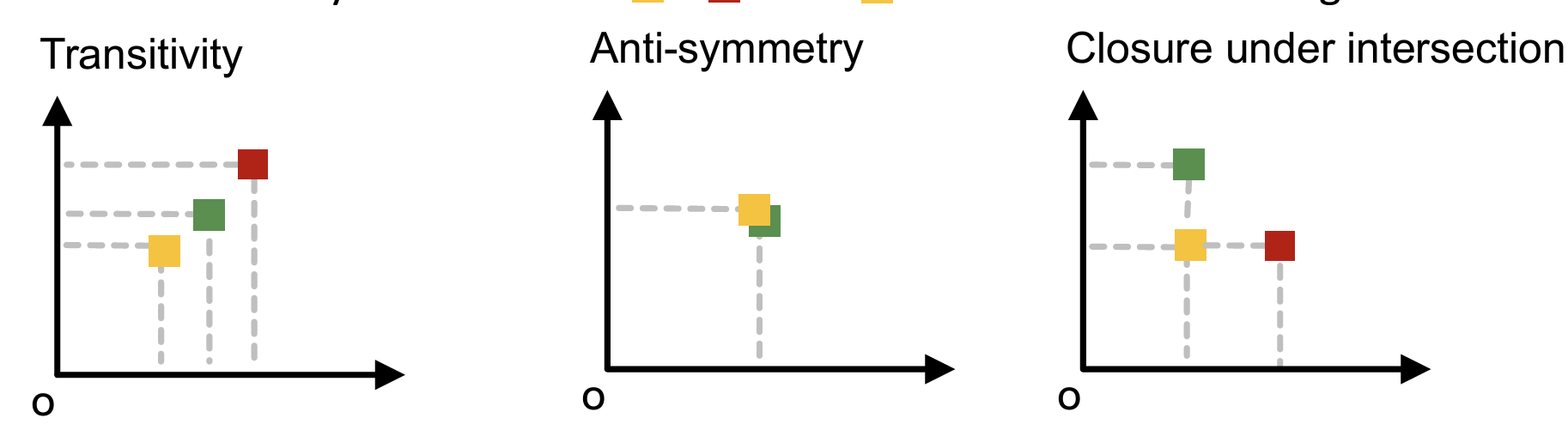
- 核心思想:把所有的图嵌入为高维向量,把子图同构的关系转换为向量的所有维数均小于的关系。
- 优点:
- 这种嵌入空间可以表示子图同构的关系,符合传递性、反对称性等要求;
- 由于空图嵌入为0,并且空图是所有图的子图,所以所有图嵌入向量应该是全正向量。

如何训练?
利用GNN对查询图和目标图进行嵌入。
构建训练样本,包括正样本和负样本:其中正样本包括一个查询图$G_q$以及一个目标图$G_t$,并且查询图是目标图的同构子图,可以通过BFS等策略进行构建。
最大化边缘损失。只有当任意维数不符合小于条件时,存在损失。
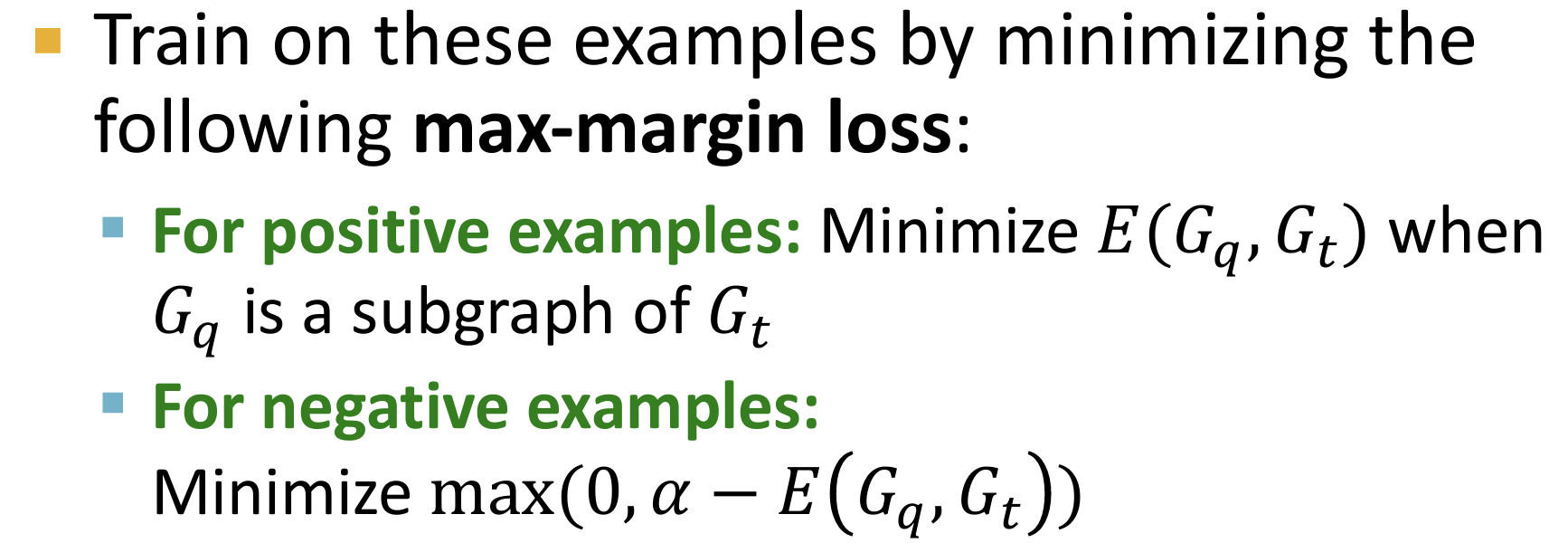
如何找出 Frequent SubGraphs【即 motifs】
- 一般的办法是:枚举一幅图的所有相同size的子图,然后数其中motifs的数量。[computationally hard]
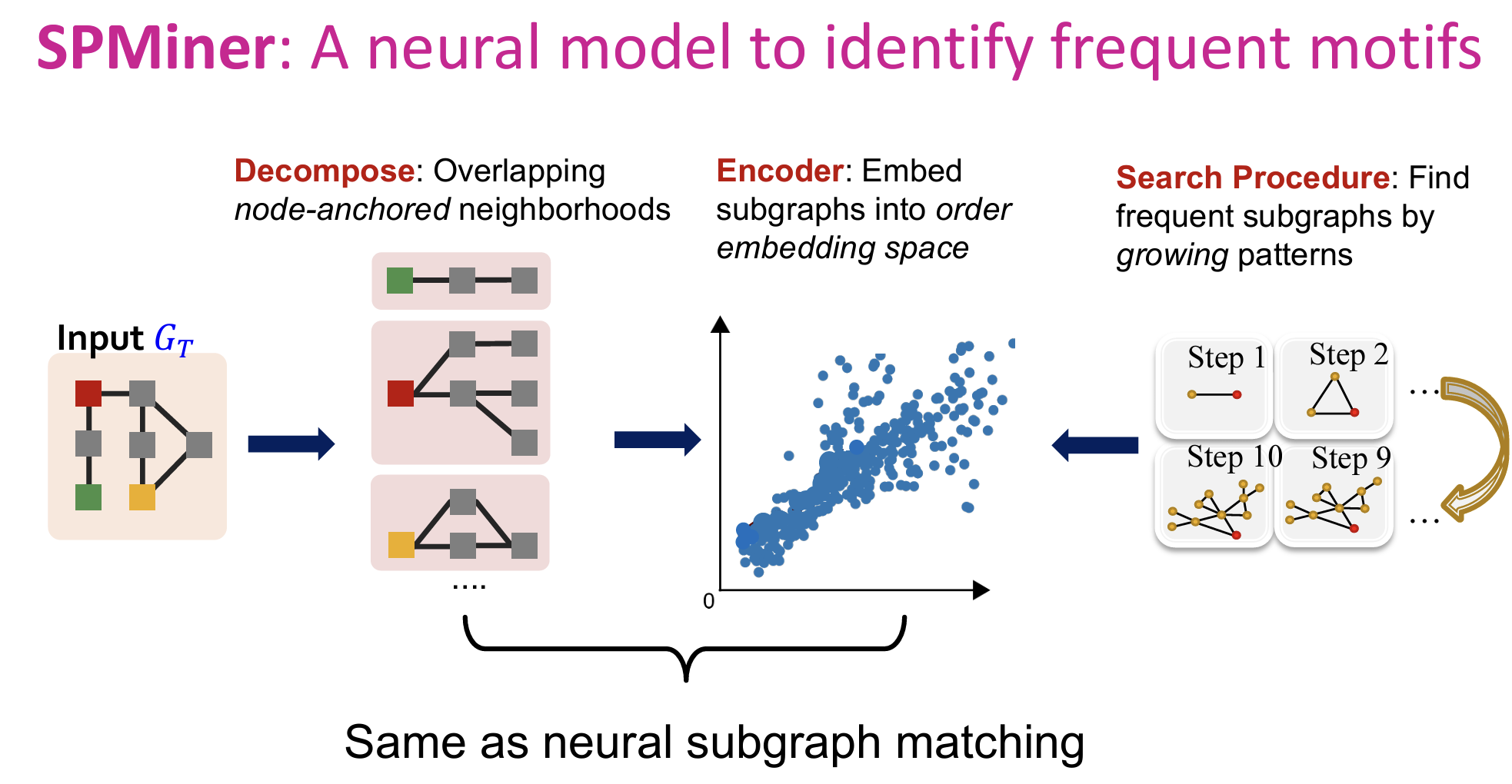
SPMiner
- SPMiner 使用神经网络模型将图结构分解、编码,并通过模式增长搜索频繁子图。
- 将图 ( G ) 分解成节点锚定的重叠邻域。具体来说,即围绕每个节点及其邻居构造一个子图,这些子图可以彼此重叠。
- 将这些子图嵌入到一个有序的嵌入空间中。
- 搜索过程:通过扩展模式来找到频繁子图。
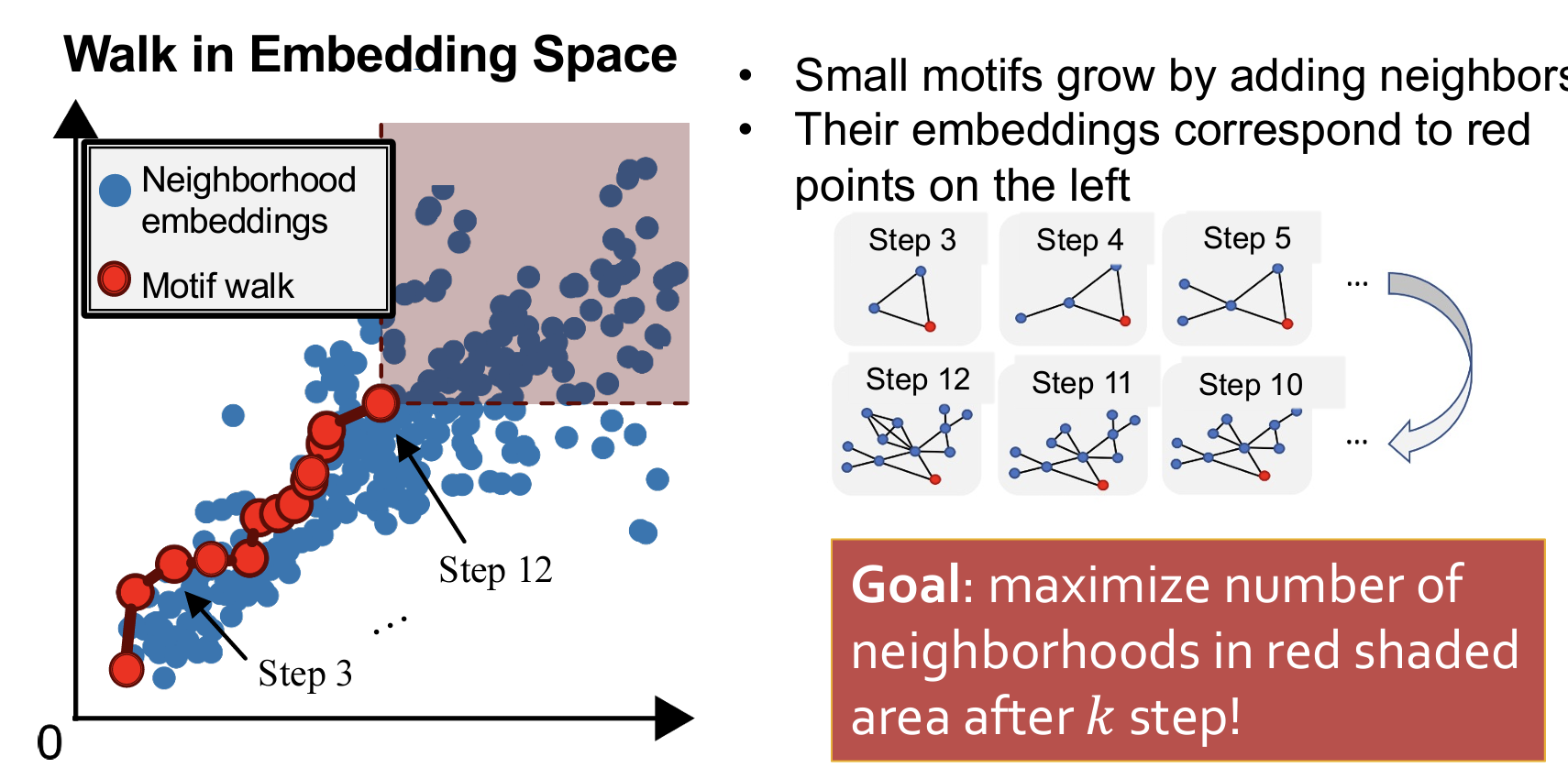
- 第三步:搜索过程详解
- 从初始节点出发,每一步进行扩展。目标是在指定的k步之后,其右上方区域的节点数量最大化。
- 简单来说,就是找到一种最优的游走方法,使得右上方区域的节点数量最大化(代表该motif是最多出现的子图模式)。
- 每一步该如何选择:启发式规则:例如贪心(每次最大化)、动态规划。
Day7
利用GNN进行推荐

推荐系统中的Graph
- 推荐系统可以自然得被建模为一个user-item的二部图
- 从而使得推荐的过程作为一个Link-prediction的任务:预测user-item的缺失边从而进行推荐
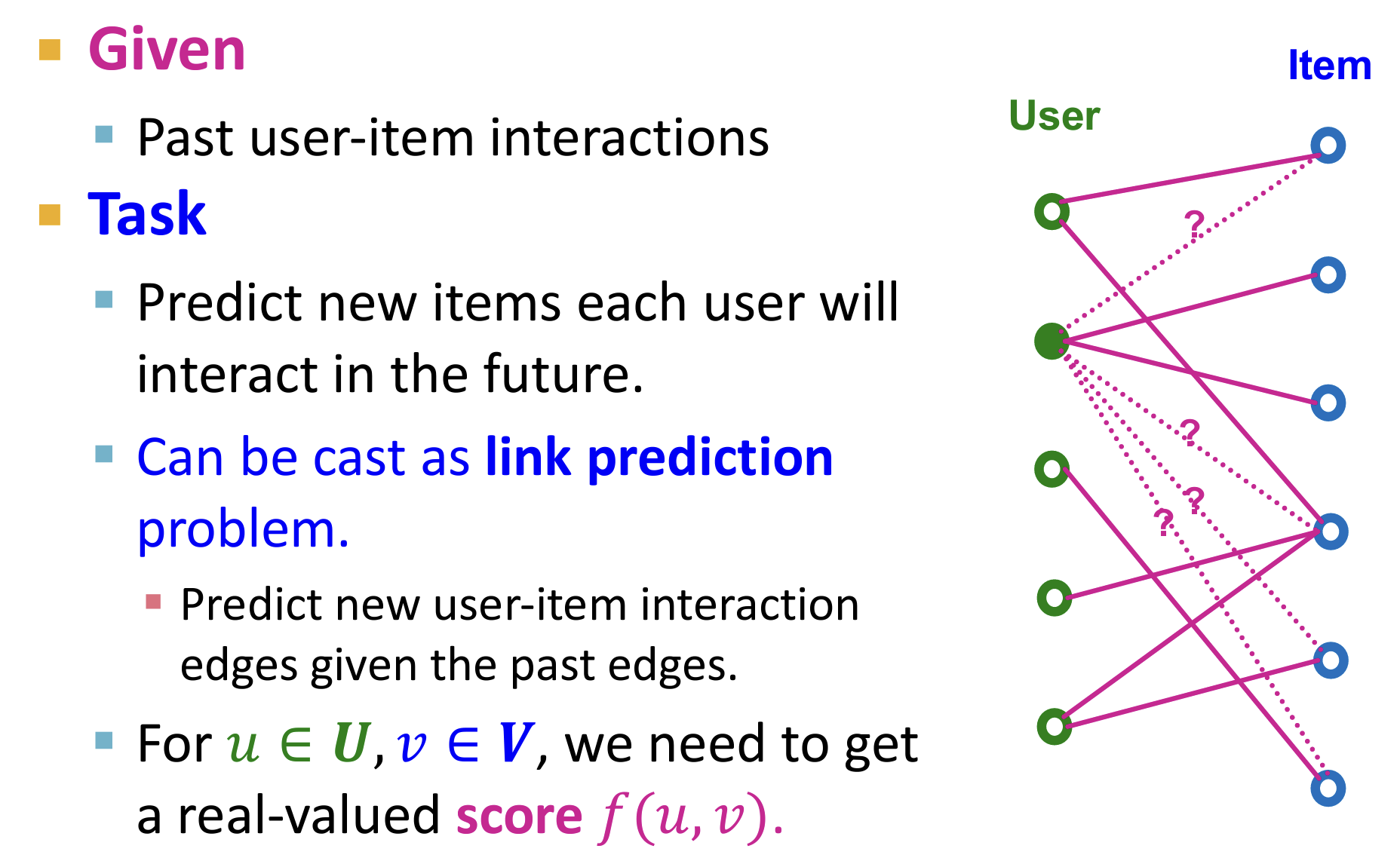
- 局限性:无法计算每个user和item之间的f分数,计算量过大;解决:使用两阶段方法,即先召回后排序
Embedding-based models
为了实现 u 和 v 之间的 score,将 u 和 v 嵌入相同维数的向量空间
训练目标:使得 recall@K 召回的成功率最大。(但这是不可微分的,无法使用梯度下降进行优化)
ML-based的优化目标要求可微,可以使用等价的优化目标[surrogate loss functions],which should align well with the original training objective[这应该与最初的优化目标非常一致。]
Binary Loss
- 对于正负样本而言,就是一个二分类问题。
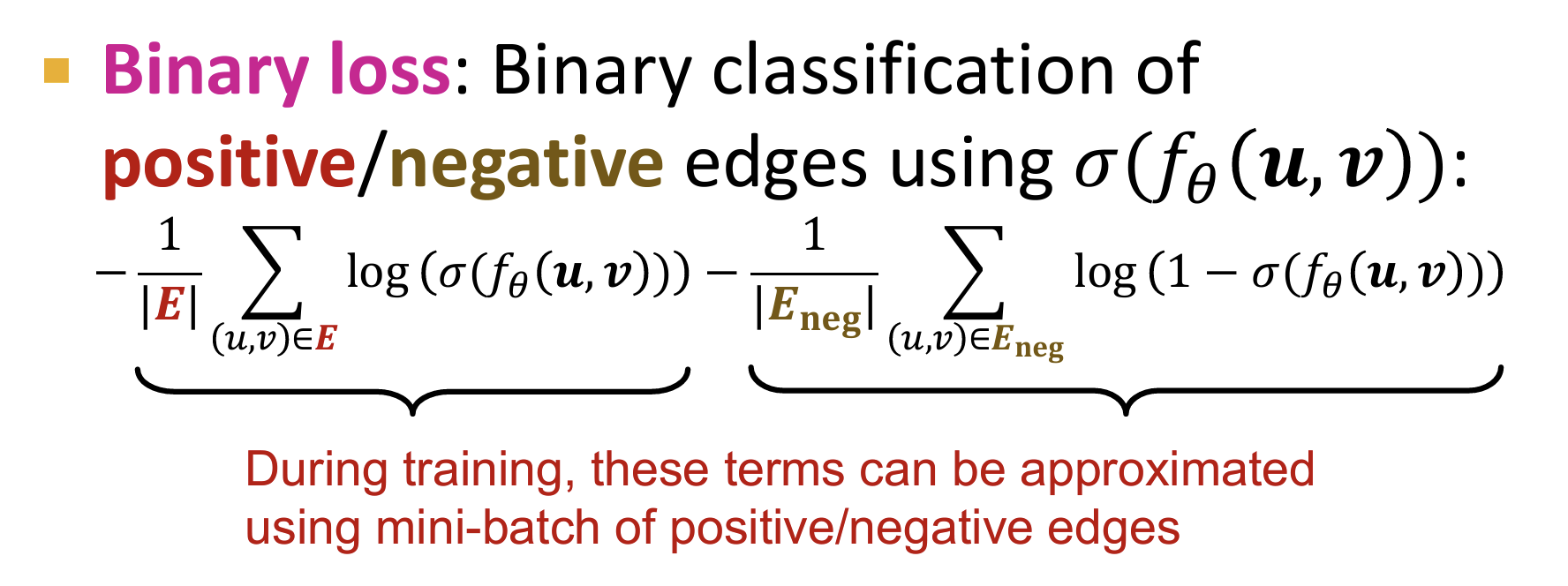
- 局限性:这样考虑所有user的loss之和,没有考虑user之间的个性差异。
Bayesian Personalized Ranking (BPR) loss
- defined in a personalized manner.
- 对于每一个user分别计算损失,目标是使得正边分数减去负边分数尽可能大

性能:
- Embedding-based models have achieved SoTA in recommender systems. [性能很好]
- 为什么 Embedding-based models work well?
- 潜在的思想:利用协同过滤的思想,对一个user的推荐借助了其它特征相似的user。
- embedding 进行嵌入实际上是嵌入为相对低维的向量,这种低维的向量无法对所有的用户/商品特征直接记忆或者建模,必须通过捕捉到其相似性/相似特征,这也是vector-embedding的优势和作用所在。
representative GNN approaches for recommender systems
传统的协同过滤方式[使用简单的binaryloss作为优化目标进行优化]:通过score function训练vector encoder,这种方法比较shallow浅层,无法捕捉到高阶的图结构信息[例如多跳信息]。
两种优化方法:(1)NGCF:使用GNN捕捉u-i二部图的多跳结构信息 (2)
一、Neural Graph Collaborative Filtering (NGCF)
- 主要的思想是通过GNN来学习user/item的embedding向量,从而捕捉到更深层次的图结构信息[High-order graph structure is captured through iterative neighbor aggregation.]。【例如对于GNN可以通过一个item来连接不同的用户,从而捕捉该信息】
- 框架:

- 其中的item/user embedding以及GNN parameters 都是可以学习的。
二、LightGCN
论文🔗:LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation
一种简化版的图卷积神经网络(GCN),专门用于推荐系统。与传统的GCN相比,LightGCN通过简化模型结构,去掉非线性激活和特征变换部分,使得模型更加轻量级且易于训练,同时保持了推荐效果。
- 动机:前述的 NGCF 同时迭代学习:(1)item/user embedding (2)GNN parameters
- 存在问题:embedding的参数量 >> GNN的参数量 [原因:embedding参数量达到(#user/item * embedding dim),其中#user/item非常非常大],说明embedding已经有足够表达能力,试图消除GNN中的可学习参数。
- user-item二部图的邻接矩阵、Embedding矩阵:
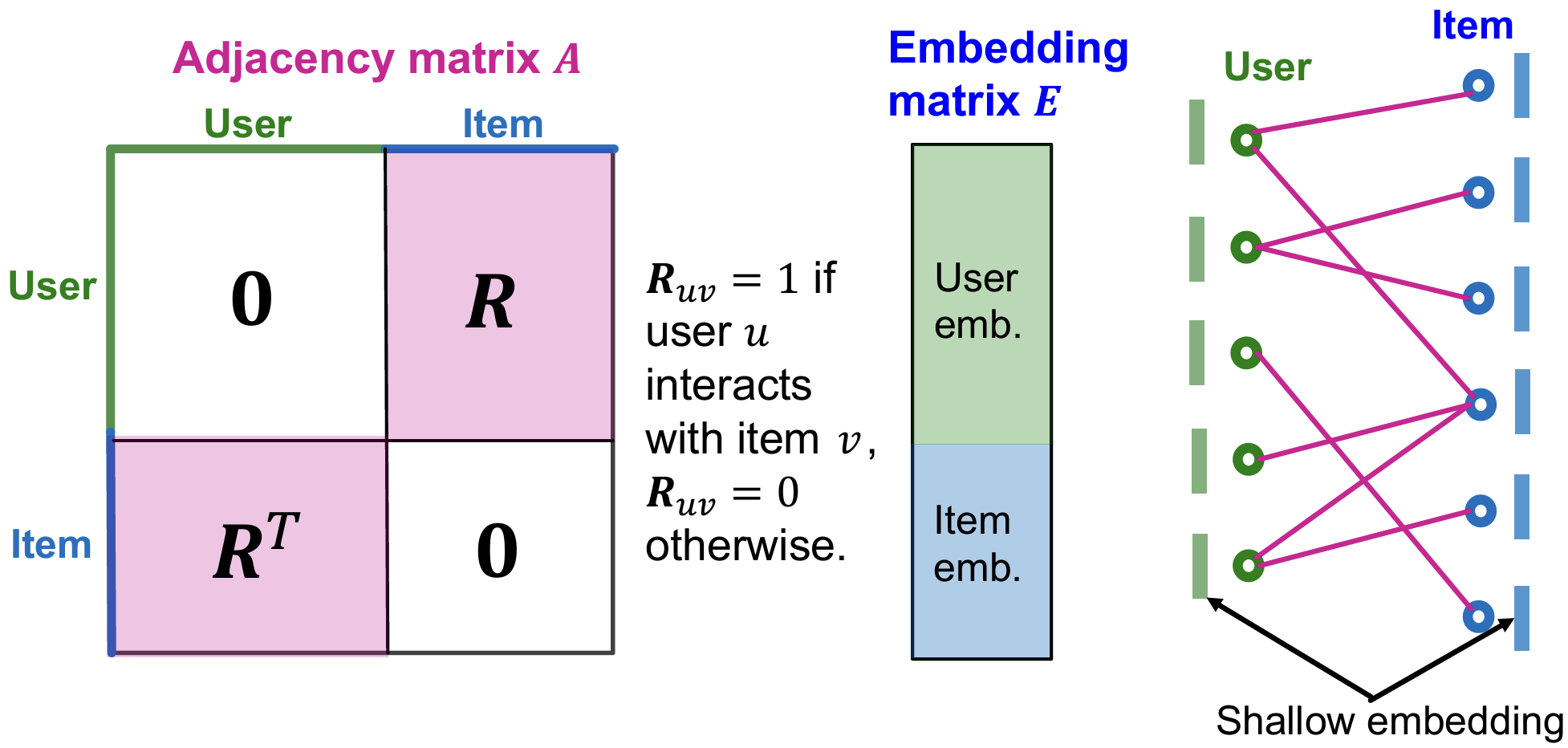
- LightGCN直接把GCN中的非线性激活、特征变换部分、自信息部分删除[作者通过消融实验验证了这个部分是没有帮助的]
- embedding的传递仅通过邻居节点embedding的聚合实现【不包含自信息部分】,并且这个聚合使用平均效果就已经很好了。
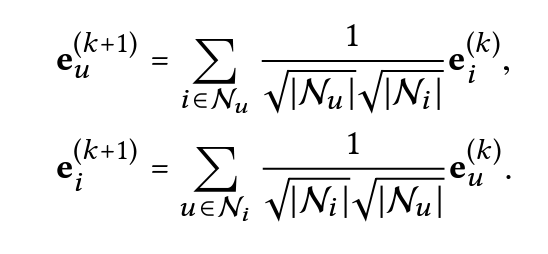
- 最后的embedding通过每一层计算的embedding的加权进行计算:
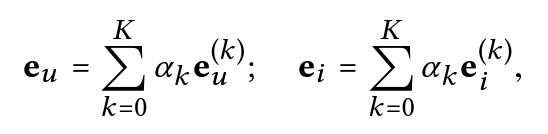
如何将扩展到大规模的推荐系统中?PinSage
Pinterest 是一款类似于微博的社交软件,需要推荐超大规模(web-scale)的数据。PinSage成功应用在了Pinterest的推荐系统
- 主要的思想类似于 GraphSAGE
- 主要的改进包括:
- 对比学习的思想:选取两篇博文作为样本,相似的作为正样本。学习目标在于将相似样本的嵌入空间尽可能接近,否则尽可能远离。
- 不使用全部的邻节点,而是进行采样。并且和GraphSAGE不同的是,进行重要性采样,即根据重要性排序后进行top-n采样。
- 在BRP损失中,需要为每一个user采样负样本,开销较大。这里使用了Shared negative samples across users in a mini-batch,即负样本共享的方法,所有用户共享负样本,只采样一次。
- 由于推荐系统在工业上需要进行细粒度的召回[从百万中取回数十商品],所以随机采样的negative samples过于简单,导致推荐系统性能比较差。PinSage使用了Hard negative samples的方法,迫使模型可以区分困难的负样本。
- 如何生成困难的负样本?从用户节点进行随机游走打分,找出关联度较高但不是最高的节点。

- 渐进式训练(Curriculum training):如果训练全程都使用hard负样本,会导致模型收敛速度减半,训练时长加倍,因此PinSage采用了一种Curriculum训练的方式,即第一轮训练只使用简单负样本,帮助模型参数快速收敛到一个loss比较低的范围;后续训练中逐步加入hard负样本,让模型学会将很相似的物品与些微相似的区分开,方式是第n轮训练时给每个物品的负样本集合中增加n-1个hard负样本。
Day8
Deep generative models for graphs

图生成问题
- 使用图生成模型进行图生成;
- 实际应用:药物发现等;
在图的生成模型(Graph Generative Model)中,p_data(G) 和 p_model(G) 是两个重要的概率分布概念,用于描述不同来源的图 ( G ) 的生成过程。
- 数据分布:
- $p_{data}(G)$ 表示真实数据的图 $G$ 的分布,也就是从真实世界的图数据中提取的分布。这个分布反映了自然界或某个特定领域中实际存在的图结构的统计特性。
- $ p_{model}(G)$ 是生成模型对图 $G$ 的分布。它表示生成模型在学习了训练数据后,生成图 $G$ 的概率分布。
- 图生成模型的目标是通过训练,使 $p_{model}(G)$ 尽可能接近 $p_{data}(G) $(密度估计),从而生成与真实数据分布一致的图;并从该分布中采样进行图生成任务(采样)
- 针对上图中Goal部分的两个目标(密度估计以及采样),提出以下两个方法:
- 如何使得$ p_{model}(G)$ 尽可能接近$p_{data}(G)$ ?最大似然概率,找到参数使得生成已观测的数据分布的样本的概率最大化。
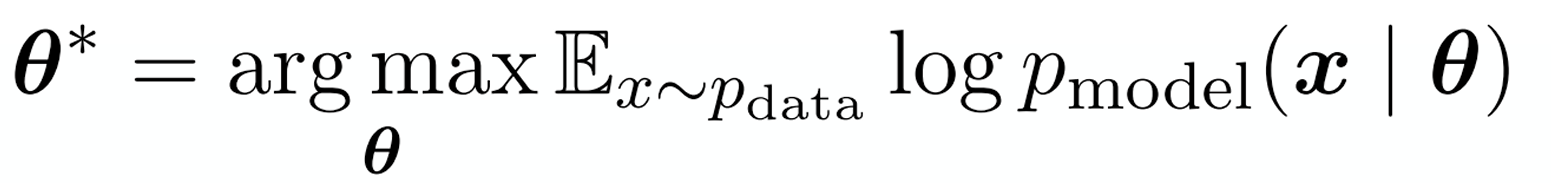
如何从$ p_{model}(G)$ 中进行采样?通过对随机单位噪声采样,通过model对噪声进行变换,使得其符合目标复杂分布:

将图的生成过程建模为一个序列的生成过程
- 一个图的生成过程有两个层次:Node-Level 以及 Edge-Level,即从点和边的两个添加过程。
- Node-Level:每一次添加一个节点。
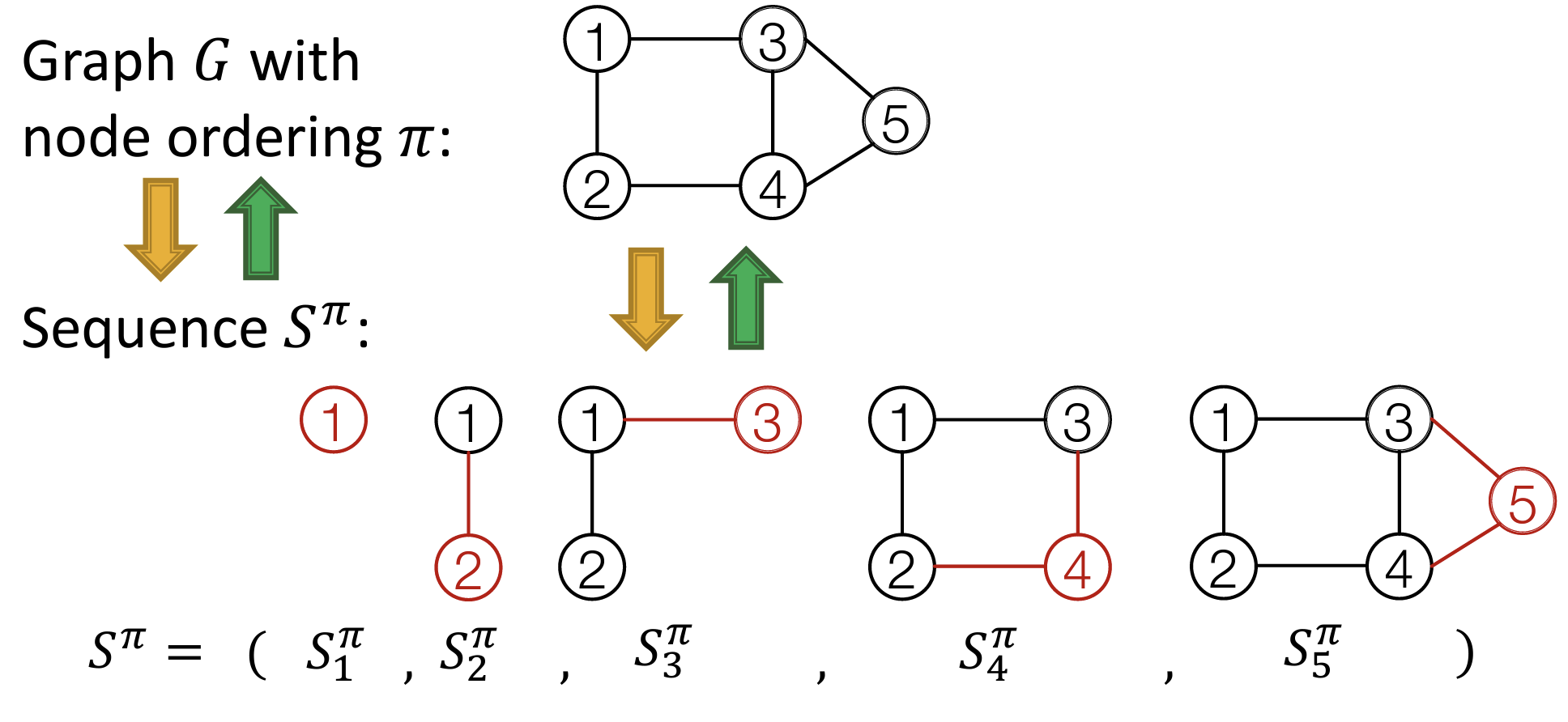
- Edge-Level:每一次对添加的一个节点连接其和其它节点的边,这是一个序列。例如,在添加节点4后,将其和其它三个节点的边建模为一个序列。
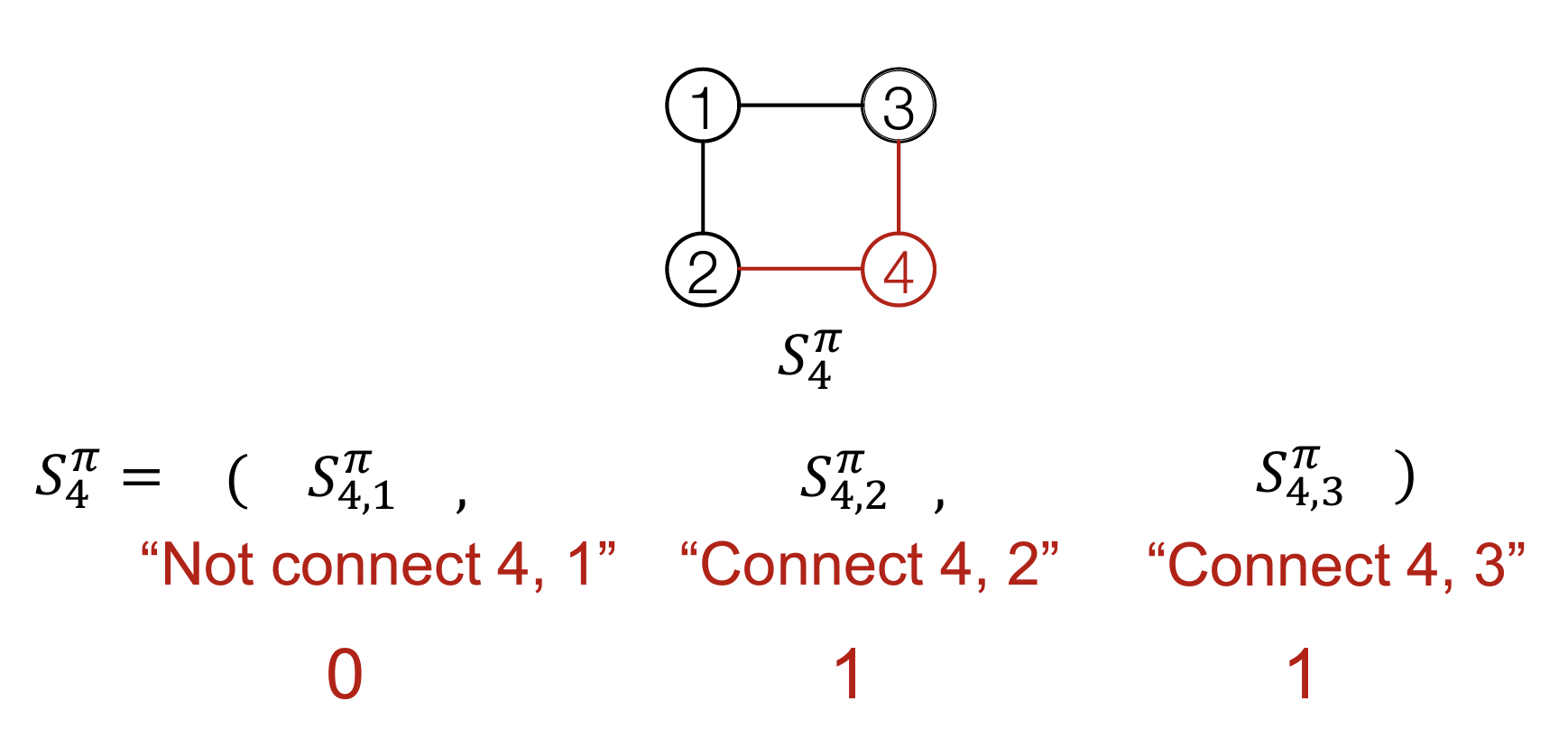
这样可以将图的生成建模为一个二维序列的生成过程。
直觉:使用序列生成模型
使用RNN进行序列生成:GraphRNN
- 使用两个RNN:NodeRNN以及EdgeRNN,分别用于生成节点序列以及连接边序列
- 工作原理:

- 分别使用SOS以及EOS token作为RNN的开始和结束的标志。
- 每一次的Edge-RNN的生成结束后,需要将Edge-RNN的Hidden State输入Node-RNN。这么做的直觉是:需要将边的连接信息输入Node-RNN来生成下一个节点,也就是说节点的生成是要依赖于边的连接信息的。
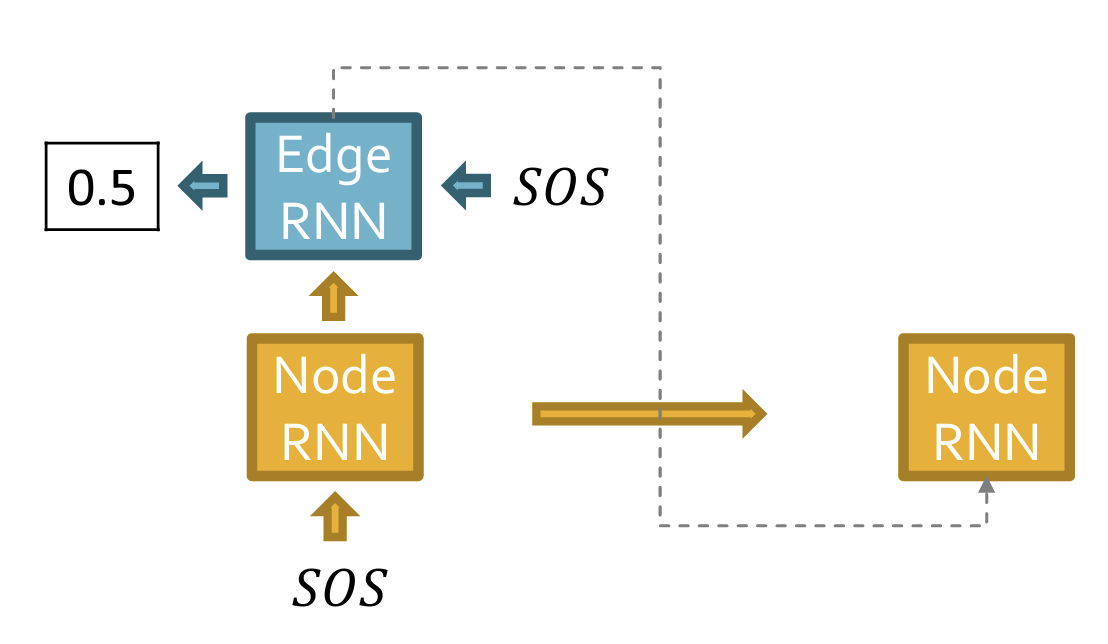
- 什么时候结束生成?当Node-RNN生成一个节点,但是这个节点在Edge-RNN中没有生成任何连接边时(如下图中的节点4所指示),说明图的生成结束。
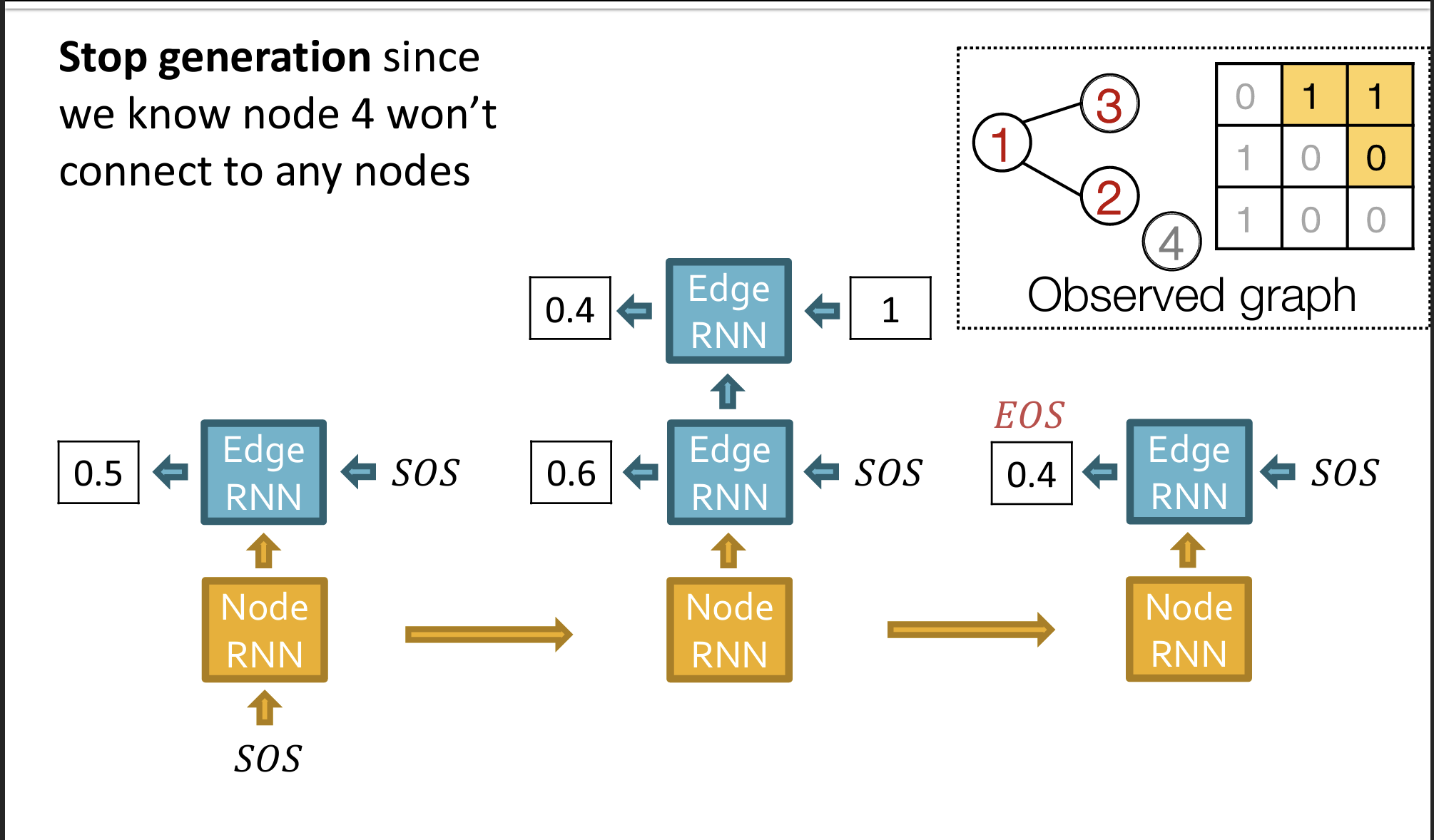
节点的生成顺序?
- 如果不规定节点生成顺序,n个节点最多有$O(n!)$多个顺序。
- 使用BFS顺序来规约节点的顺序。
评估模型生成好坏的指标?
- 视觉相似性。肉眼看起来生成的效果。
- Graph统计指标的相似性。例如节点平均度等等。
Graph Convolutional Policy Network (GCPN)
GraphRNN的局限:当需要完成一些Goal-Directed图生成任务时(要使得生成的图符合或者最优化某些目标,例如在药物发现任务中,要最大化生成图结构的类药性),GraphRNN无法做到最优化这些目标。
GraphRNN在生成图时主要关注图的结构和连通性,而不一定直接考虑生成图是否符合某些特定的优化目标。这种局限使得GraphRNN生成的图可能没有最优的性质,尤其是当目标特性与生成的图结构复杂且不直接相关时。
GCPN主要使用了图表示学习以及强化学习的技术
图生成的过程中:将节点进行Node Embedding,并进行Link-Prediction任务。
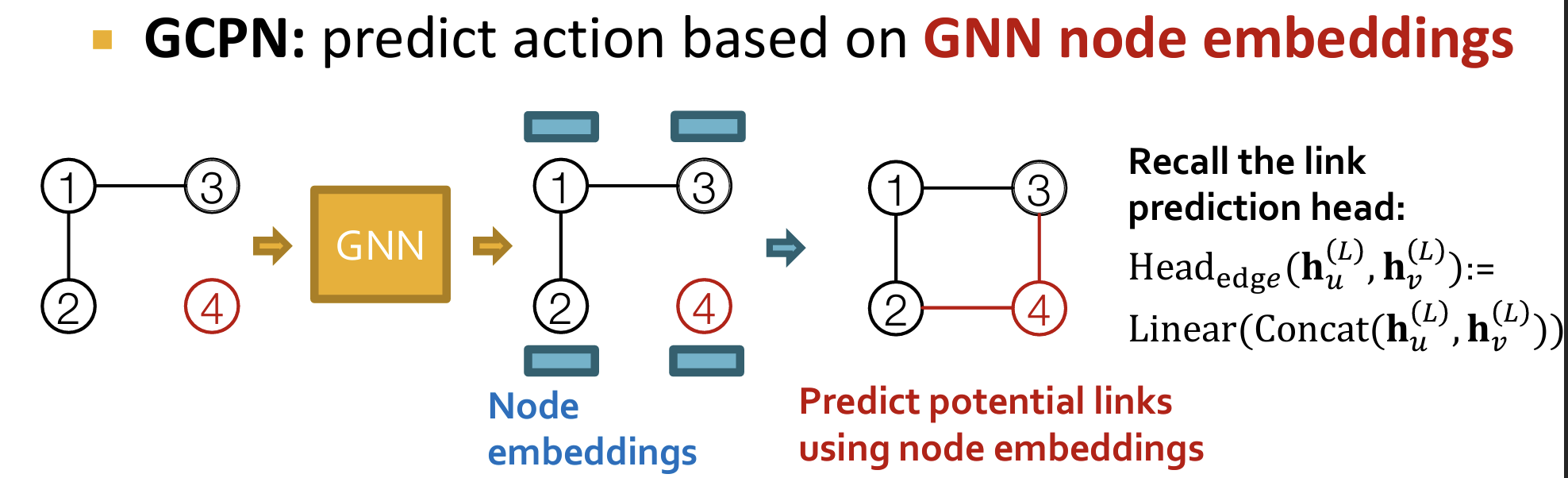
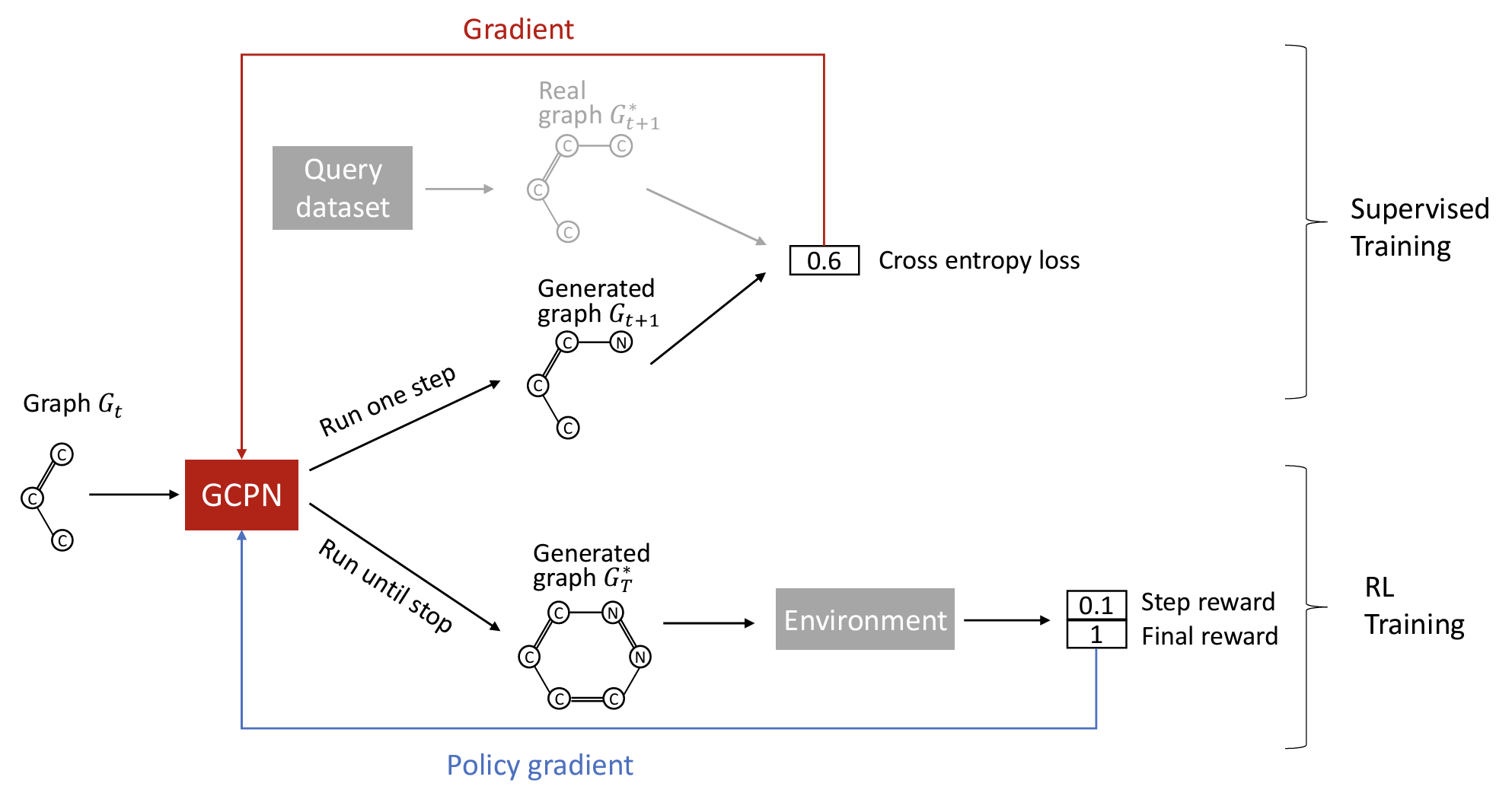
是有强化学习使得agent模型和环境进行交互,通过反馈来完成需要最优化的指标。
如何训练?两个主要部分:(1)使用给定图进行监督学习(2)强化学习。

Day8
Advanced topics in GNNs

GNNs 存在的不足之处
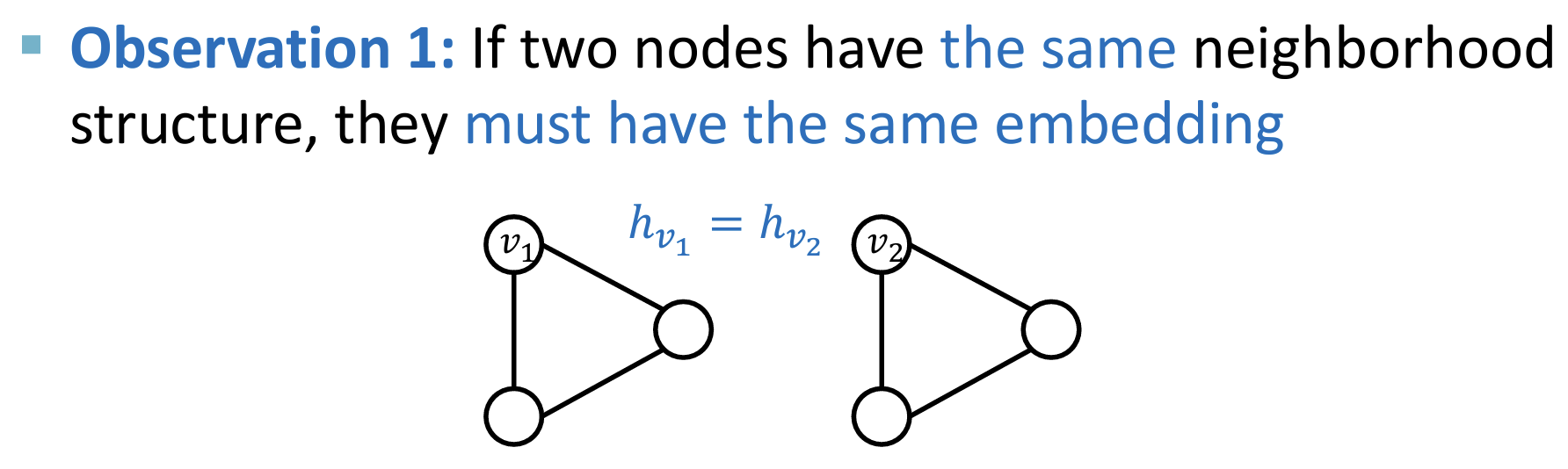
(1)GNN中,如果节点具有相同的邻结构,那么它们将总是具有相同的embedding。
- 这么做有时候是不合理的,因为有时候需要对Graph中不同位置出现的相同邻结构的节点赋予不同的embdding。
- 即:从GNN的角度来看,Graph中不同位置出现的相同邻结构的节点是不可区分的
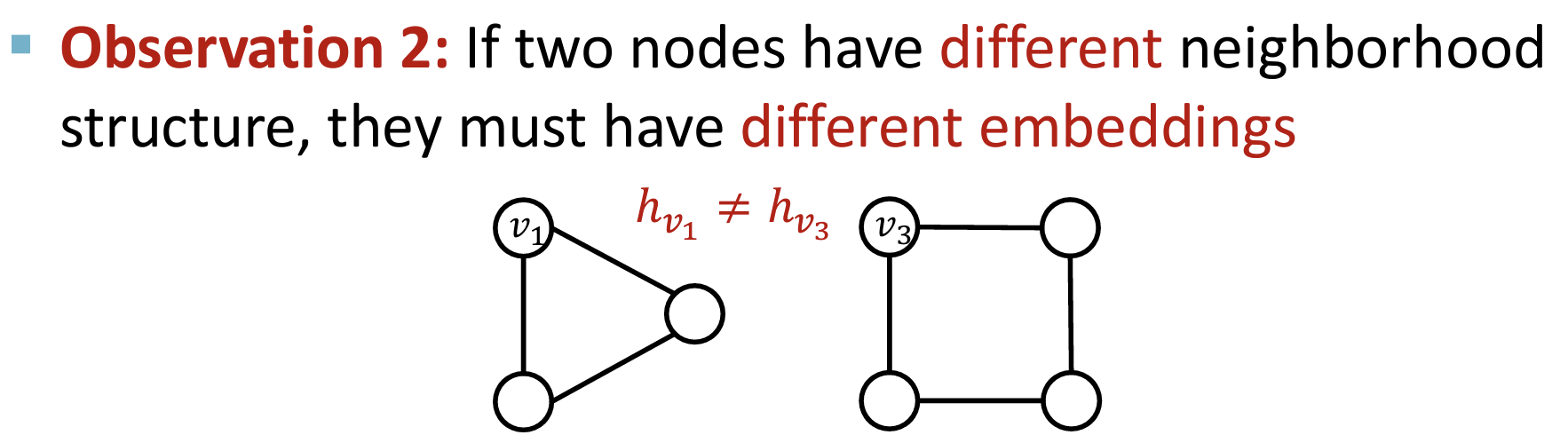
(2)原则:如果节点具有不同的邻结构,GNN需要节点具有不同的embedding。
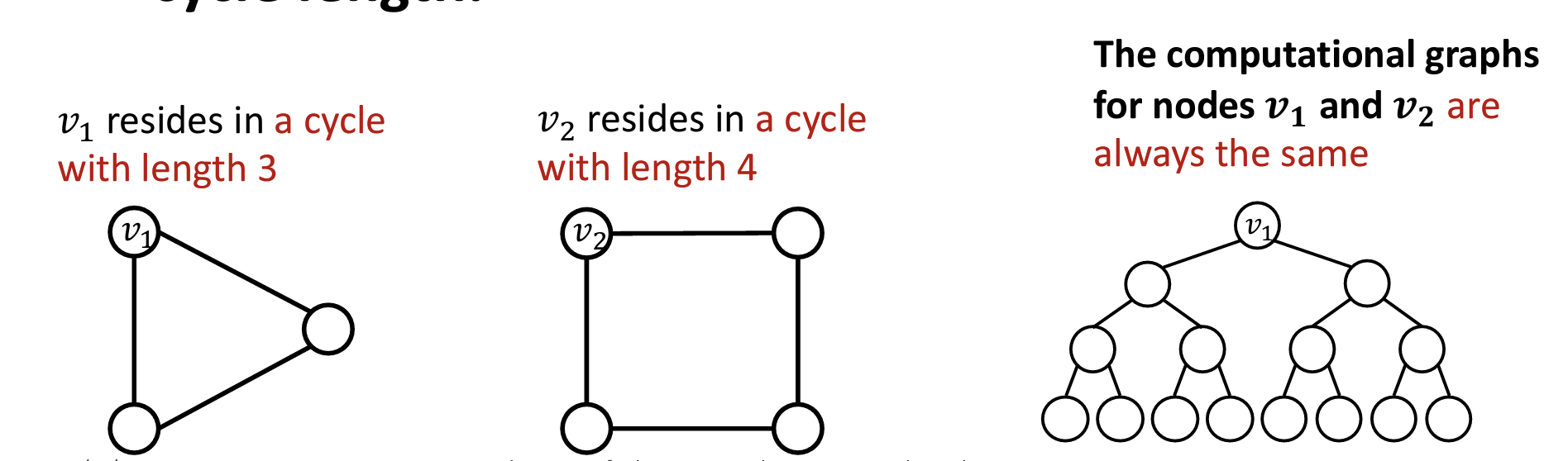
- 但是这个原则有时会被违反,例如下图所示的两个节点,由于它们的计算图一样, 所以GNN计算的embedding是一样的。
如何解决?
- 对于问题(1),引入 position-aware GNNs 使得其关注不同节点的位置信息。
- 对于问题(2),引入 身份感知GNN(Identity-aware GNNs)

Position-aware GNNs
GPT for This:
Position-aware GNNs 是一种改进的图神经网络(GNN)模型,通过增强对节点在图中位置的感知能力来提升模型的表达能力。这种方法主要解决了传统GNN模型在处理图结构时对节点位置敏感度不足的问题。
基本概念
在图神经网络中,节点的特征表示和消息传递主要基于其邻居的特征。然而,这种方法可能忽略了节点在图中的相对位置和结构信息,特别是节点与图中其他节点的位置关系。Position-aware GNNs 通过引入位置感知机制,来改进这一点。
关键特性
- 位置编码(Position Encoding):
- 定义:位置编码是将节点在图中的位置或相对位置的信息嵌入到节点的特征中。这可以包括节点的度数、在图中的路径距离或其他表示位置的特征。
- 目的:增强模型对节点在图中具体位置的感知,帮助模型更好地捕捉图的结构信息。
- 位置感知机制:
- 方法:在传统的消息传递过程中,节点的特征信息不仅仅包括其邻居的特征,还包括位置编码信息。这种方法可以通过在每层GNN中加入位置编码来实现。
- 集成:位置编码信息可以通过各种方式集成到GNN模型中,如与节点的原始特征拼接、加权求和或通过特定的网络层处理。
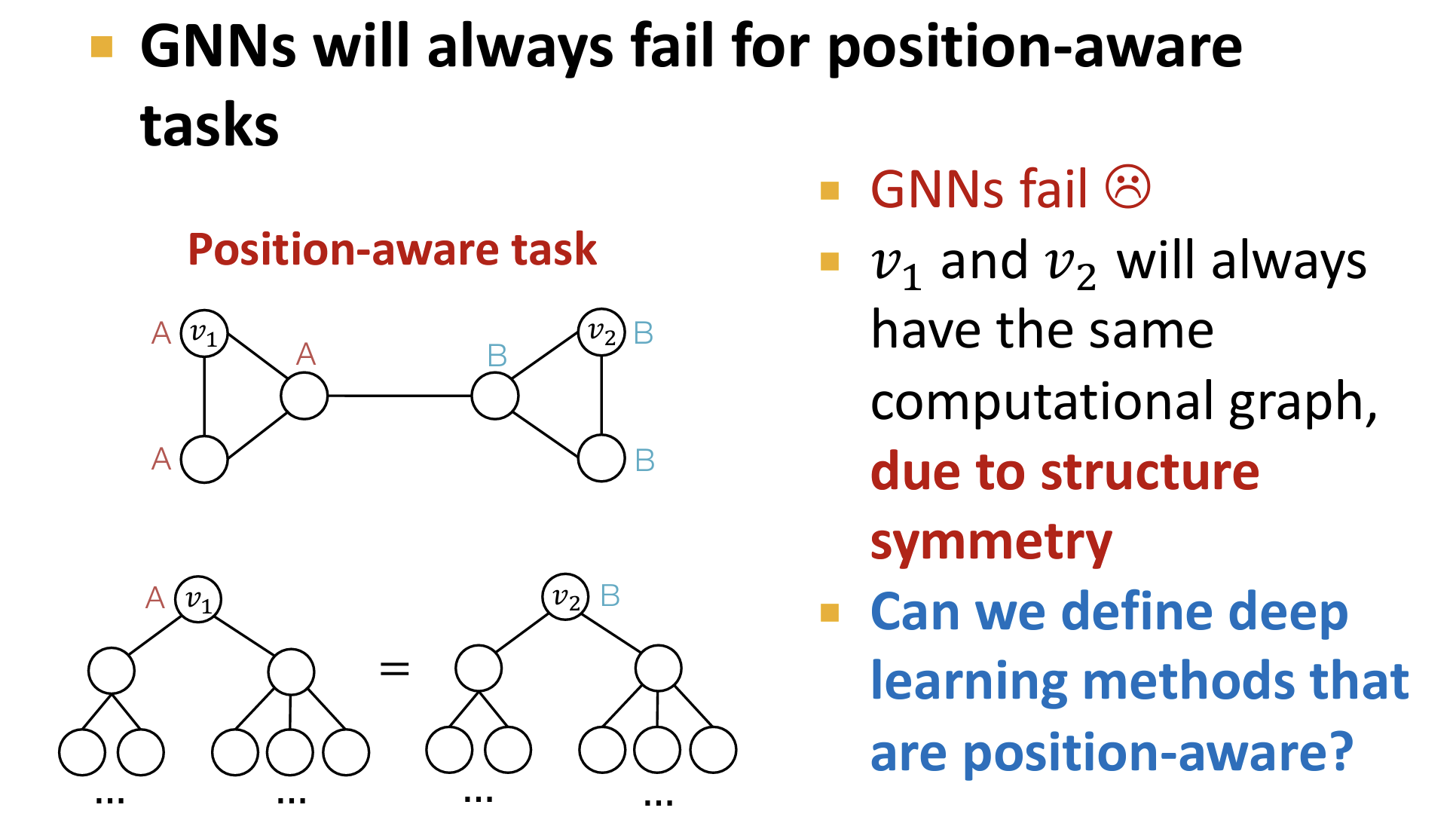
- 原因:GNNs 通常可以有效地捕捉Graph的结构信息(对于相同邻结构的节点使用相同的训练Label,并且相同邻结构的节点具有相同的计算图),但是很难捕捉Graph的位置信息。
- 在 Position-aware 的任务中,GNNs 失效。【对于相同邻结构的节点,其具有相同的计算图,但是由于处于不同的位置,其具有不同的位置标签信息】
锚点
- 选择节点/节点集合作为锚点/锚点集合,节点在Graph中的位置可以表示为:到每一个锚点的距离。
P-GNN 过程
- 样本化锚点集:选择 $O(\logn)$个锚点集。
- 节点嵌入:计算每个节点到这些锚点集的距离,并将这些距离作为节点的嵌入特征。
- 主要思想:随机采样锚点集合,并使用节点到锚点集合的距离作为节点的嵌入表征。

Identity-aware GNNs
问题:GNNs 对于不同的结构的节点,倘若其计算图相同,就会导致这些节点嵌入到相同的向量(不可区分这些节点)。这是GNNs存在的缺陷,无法识别到潜在的不同结构的图特征。对这样的节点的不可区分性,会使得GNNs在node/link/graph level的prediction等任务丧失性能。
解决:使用节点着色【node-coloring】-对节点特征进行增强:
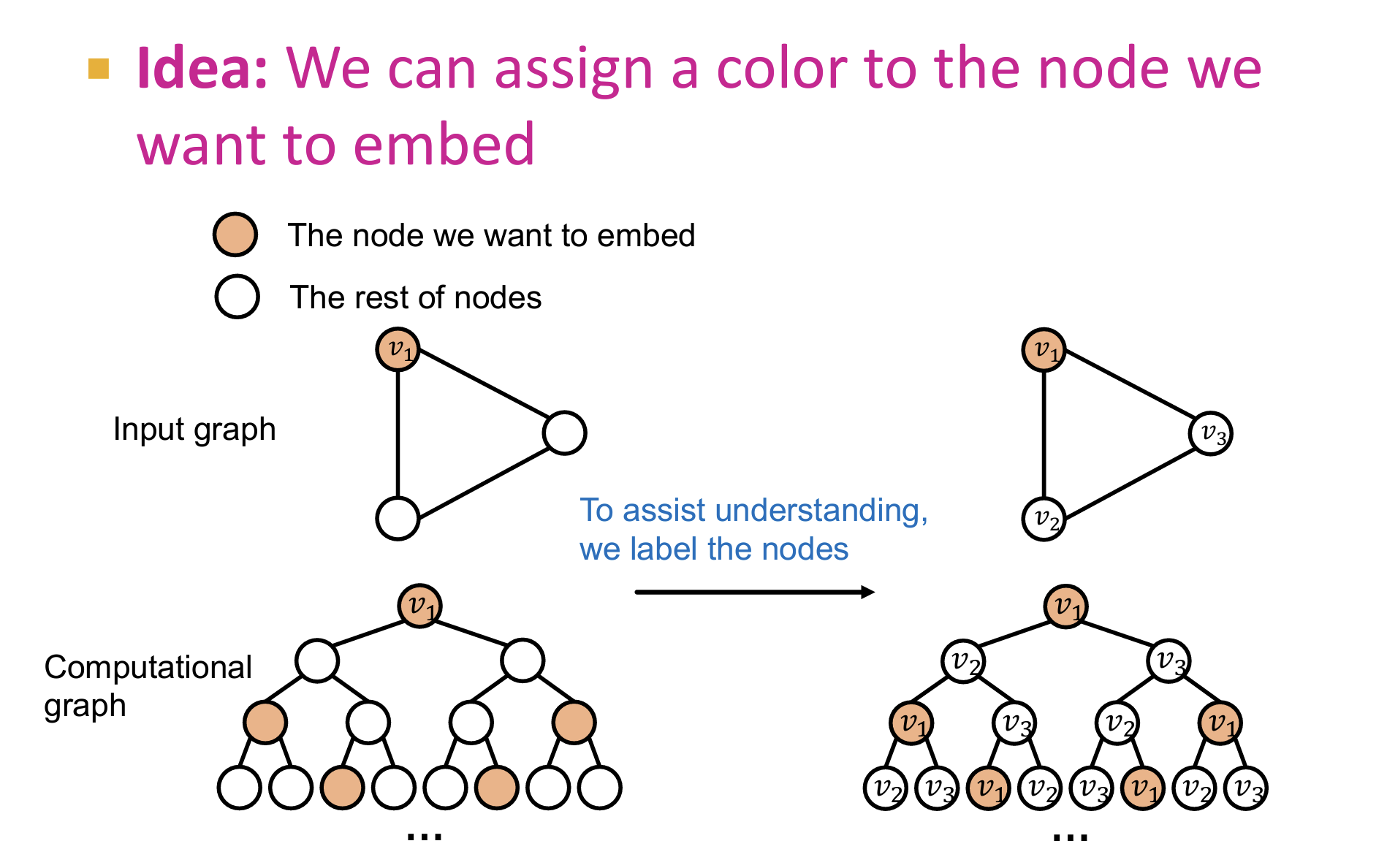
- node-coloring 是 inductive的,即可以扩展到测试集的。因为(1)其具有排序不变性质
如何在 ID-GNN 中运用节点着色的思想:异构消息传递【Heterogenous message passing】
- 通常在GNN中例如GCN,我们在同一层对所有节点使用相同的NN。
- ID-GNN中:对不同颜色的节点,使用不同的NN,即使用不同的消息传递/聚合方法。
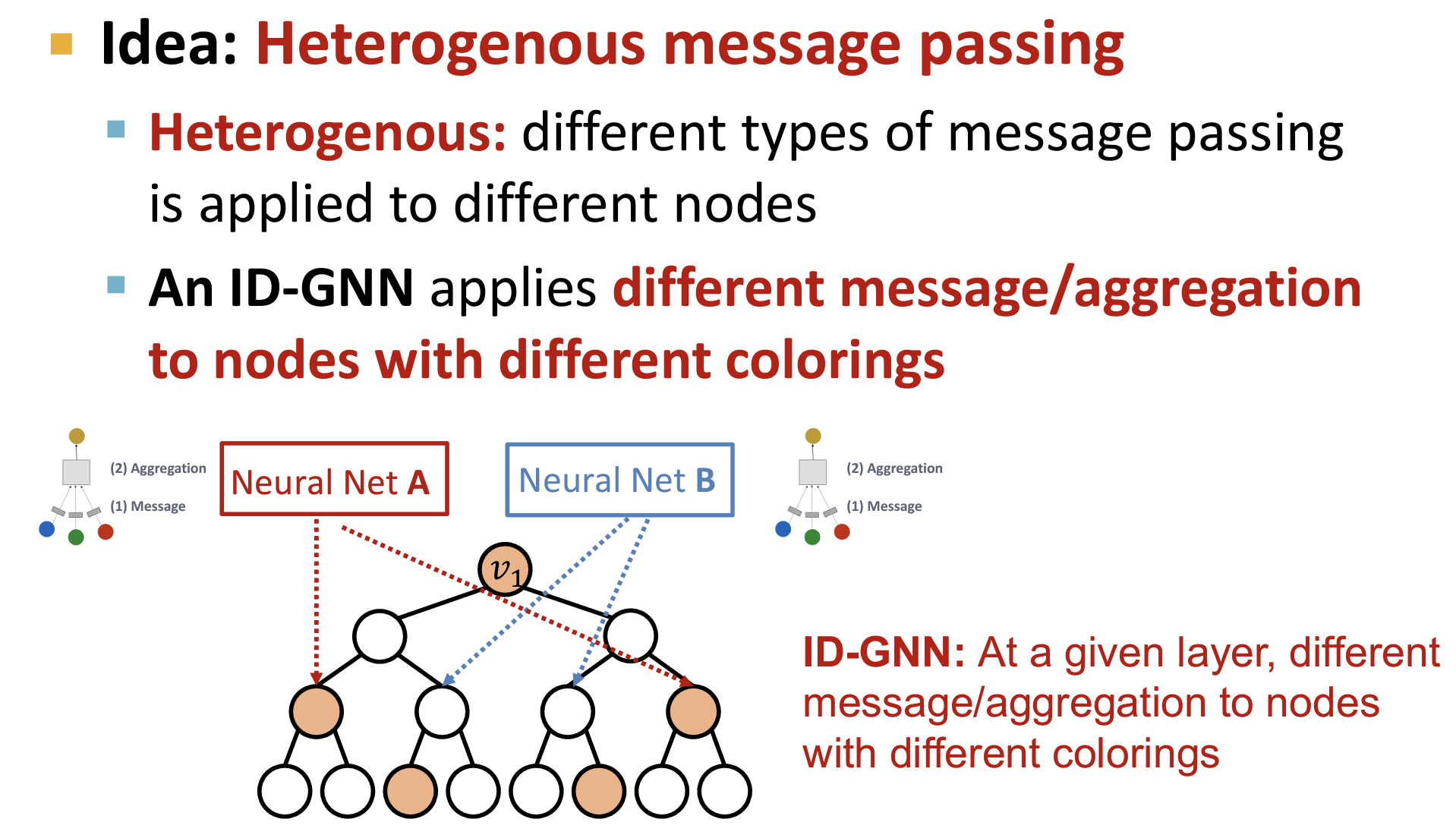
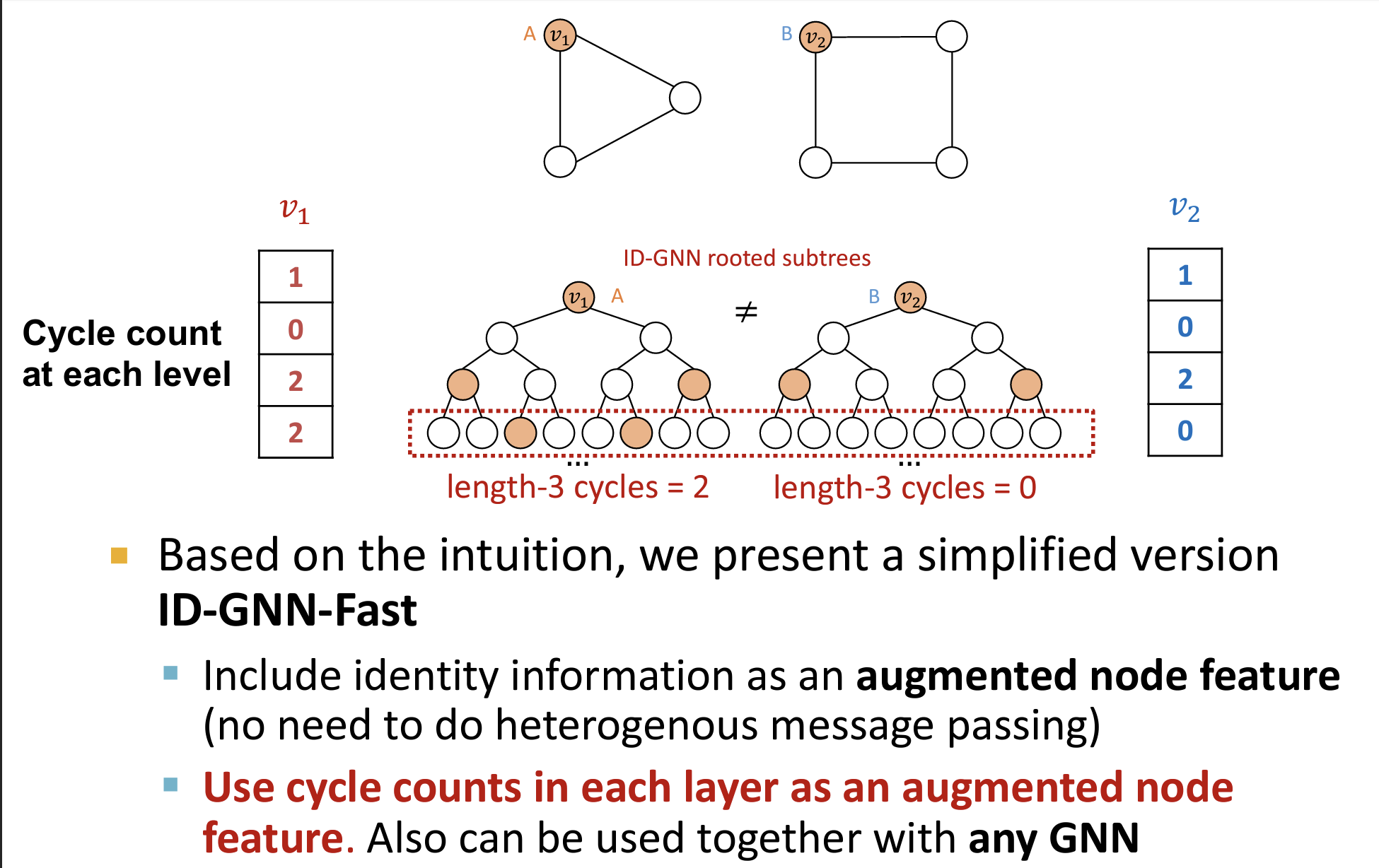
ID-GNN-Fast
- 如下图所示,计算图中每一层的着色节点数量表征着长度为层数的环的个数(例如,第三层有两个着色节点,代表图中有两个从根节点出发的长度为3的环)
- 可以将这种性质看作为节点的特征
总结
- 总的来说,ID-GNN 是 GNN框架的一种通用的强大的扩展,可以嵌入GCN、GraphSAGE …..,只需要在消息传递的时候对节点使用异构的网络。并且通常可以得到收益。
GNNs 的鲁棒性研究
- 对抗样本for GNN
- 对抗攻击:转换为一个优化问题:

Day9
Graph Transformers

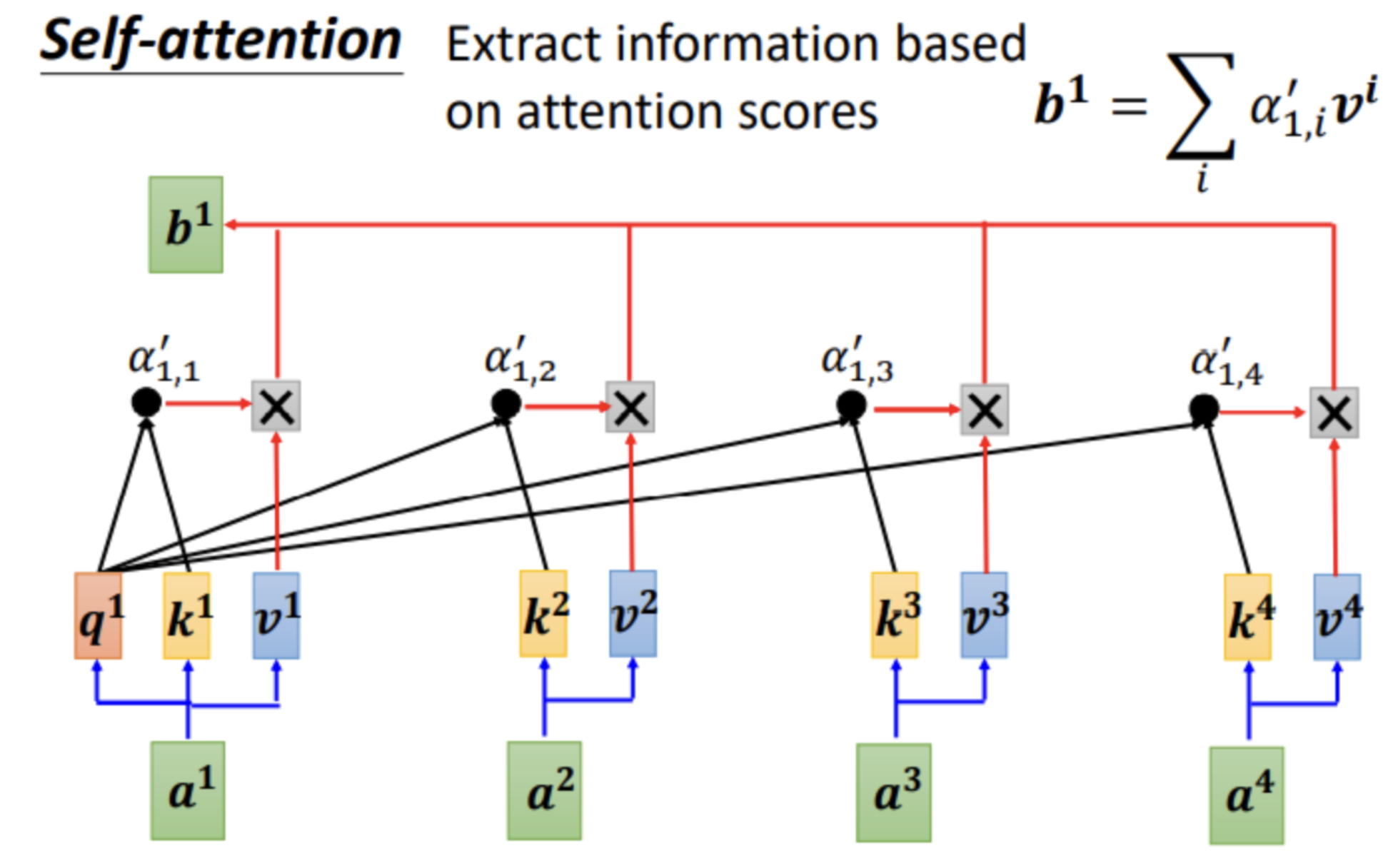
自注意力机制
- 针对每一个序列输入,嵌入为 embedding 向量。
- 使用模型参数对每一个输入计算query、key、value:
- 使用query和key计算权重分数(可以是内积之后使用softmax转换为概率),使用权重分数乘以value值,得到输出向量。
GNN v.s. Transformer
- Difference: GNNs use message passing, Transformer uses self-attention
- 自注意力的计算可以写作:通过矩阵进行并行计算
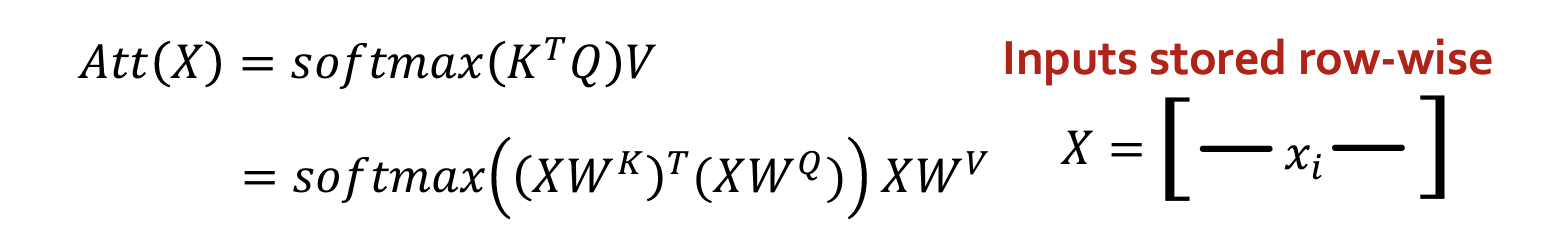
- 将上述的计算过程可以写为 MSG-AGG 的形式:

说明:自注意力就是一个 GNN,其中每一个token代表一个node
- 每一个 node,其它邻节点消息传递的方式是生成key和value。
- 自身的消息传递(自循环)是生成query。
- 使用Q、K、V对所有消息进行聚合。
显然这个GNN是一个完全图,所有的节点都相互连接。
位置编码
在任何一门语言中,词语的位置和顺序对句子意思表达都是至关重要的。传统RNN模型天然有序,在处理句子时,以序列的模式逐个处理句子中的词语,这使得词语的顺序信息在处理过程中被天然的保存下来,并不需要额外的处理。
由于Transformer模型没有RNN(循环神经网络)或CNN(卷积神经网络)结构,句子中的词语都是同时进入网络进行处理,所以没有明确的关于单词在源句子中位置的相对或绝对的信息。为了让模型理解序列中每个单词的位置(顺序),Transformer论文中提出了使用一种叫做 Positional Encoding(位置编码) 的技术。这种技术通过为每个单词添加一个额外的编码来表示它在序列中的位置,这样模型就能够理解单词在序列中的相对位置。
- 如下图所示,如果token序列的顺序改变,预测结果相同。说明预测没有考虑到token的位置顺序关系。
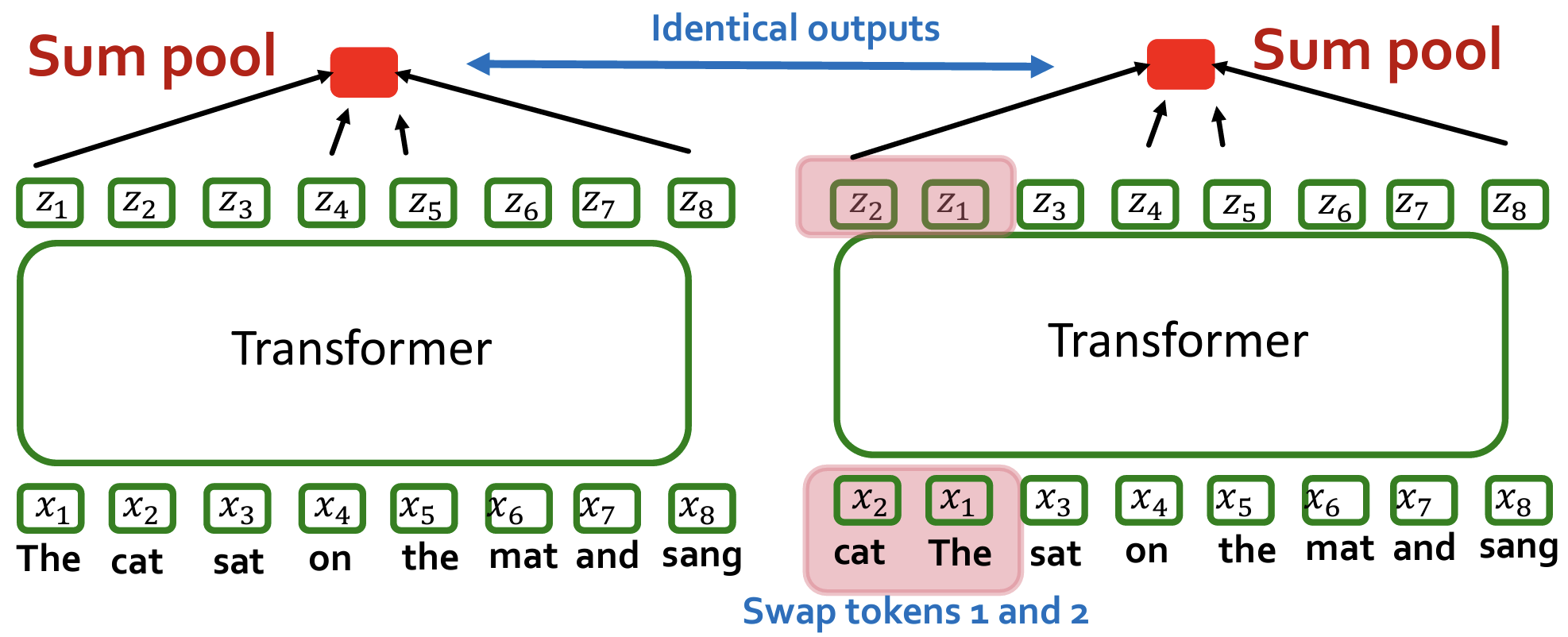
Transformer不知道token的位置关系,需要额外使用位置编码作为特征。
两种方法:
- 作为可学习的参数。
- 作为预训练的参数。
使用Transformers处理Graph
- 不同组件的对应关系如下:

- 图的节点特征 —— token
- 容易实现,只需要将node features作为transformers的输入token seq即可。
- 节点的邻接信息 —— 位置编码
- 如何实现?
- (1)使用相对距离:复用上一节课程的position-aware位置感知的GNN的思想。在图中采样锚点集合,使用节点到锚点的距离作为其位置的表征。
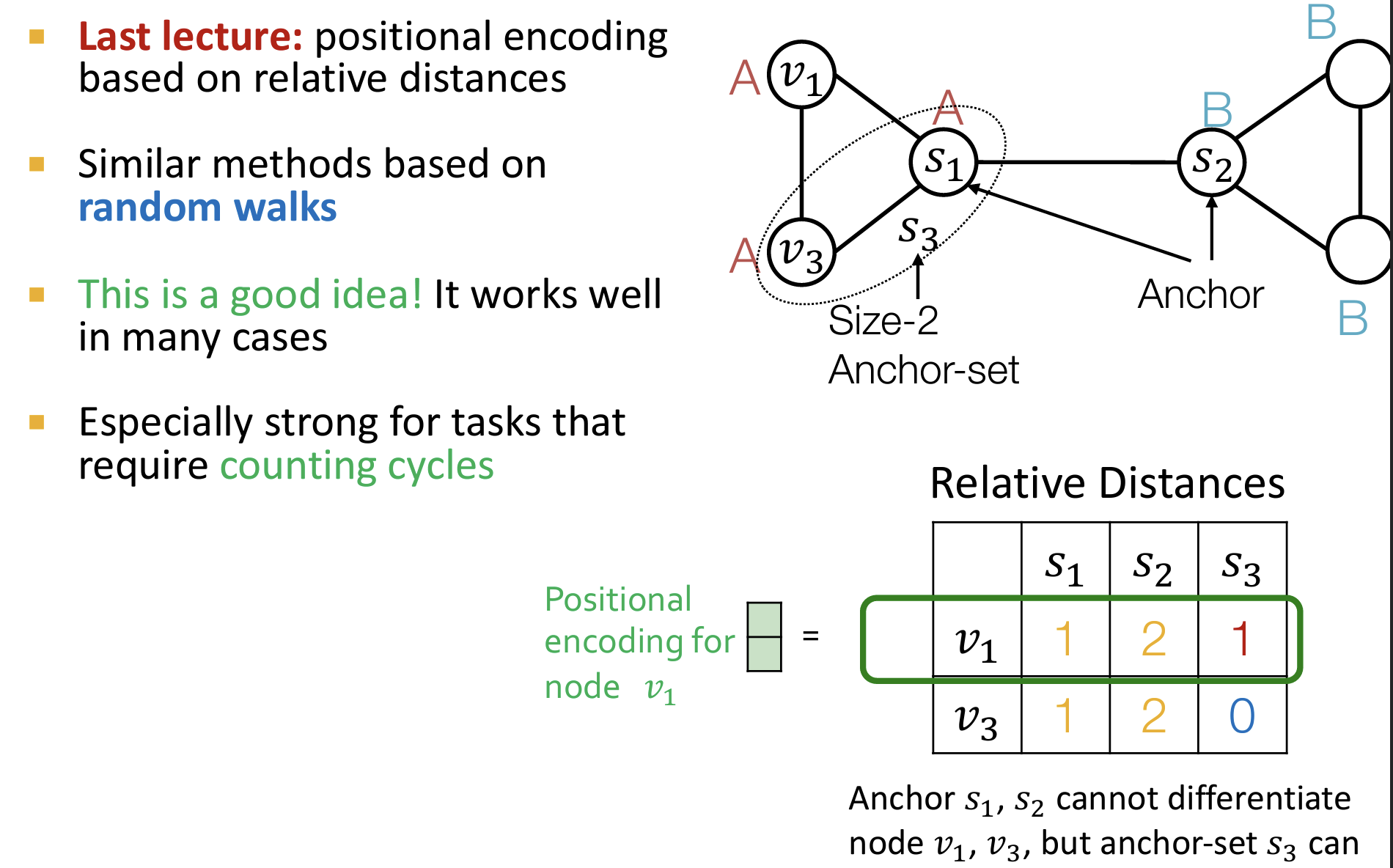
- (2)使用拉普拉斯矩阵的特征向量进行位置编码:
- 拉普拉斯矩阵?也称为调和矩阵。即度数矩阵-邻接矩阵。(它的特征值和特征向量可以提供图的结构信息,例如图的连通性和社群结构。)
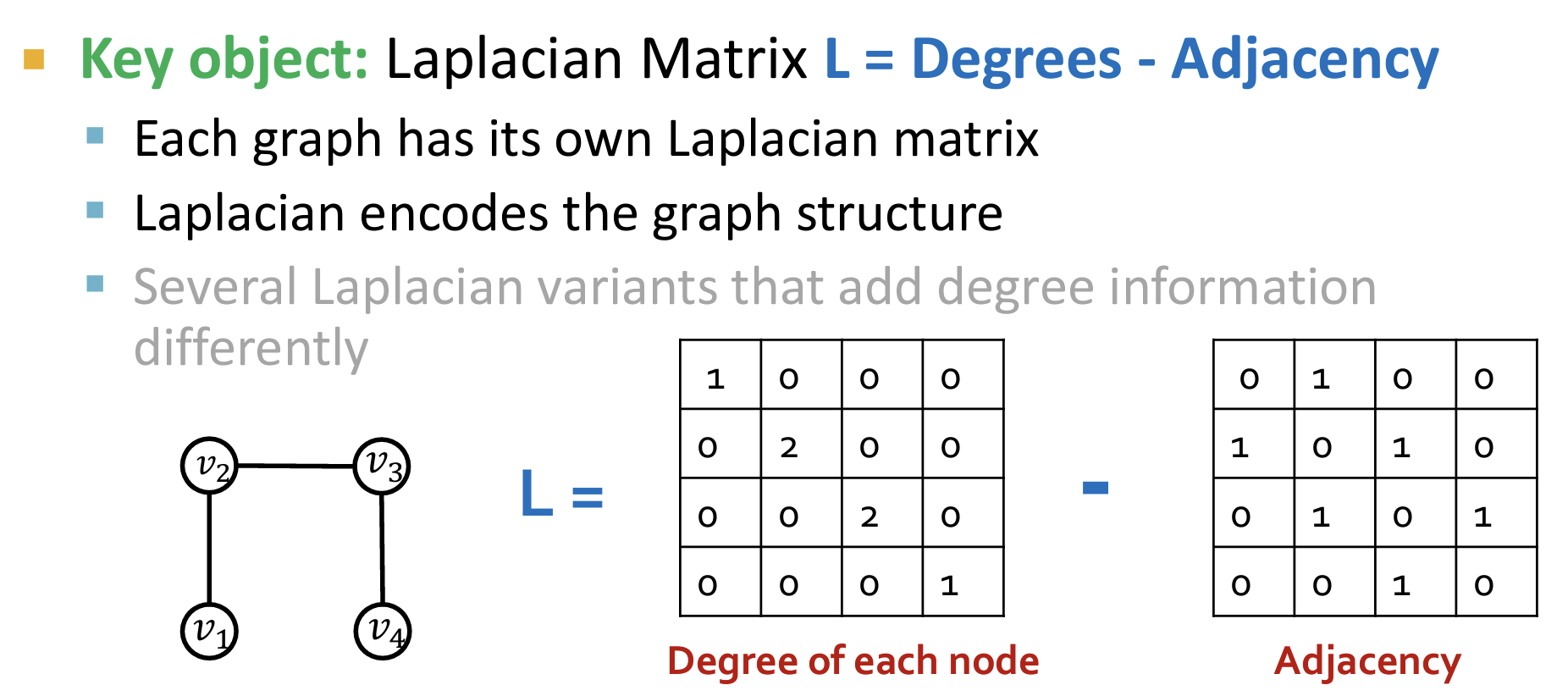
- 使用拉普拉斯矩阵的特征向量(适合transformer的向量input),其表征了图的结构信息。其中对应特征值大的特征向量表示全局结构,特征值小的特征向量表示局部结构。
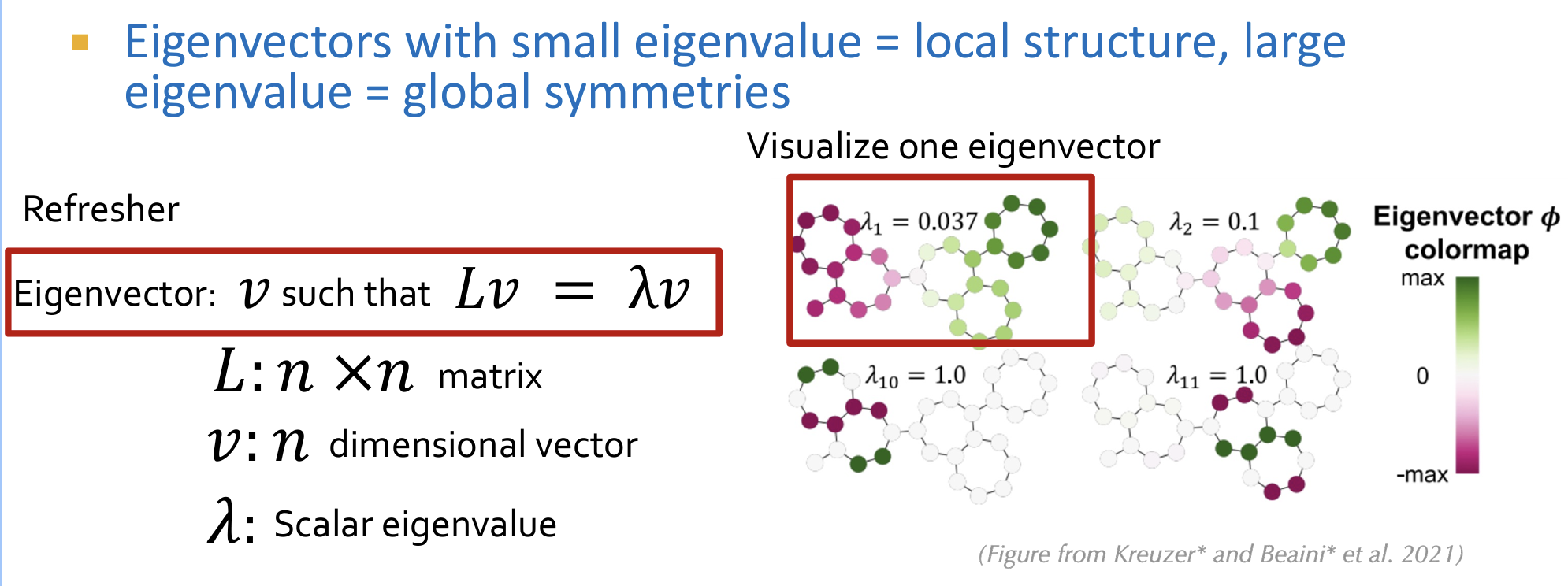
- 边的特征 —— 自注意力(自注意力使得信息在节点之间交互,所以对应连接边的作用)
- 在使用Transformer处理图时,如何考虑边特征信息?
- 如下图所示,将边的特征加入注意力的计算中:在计算了节点 i 和节点 j 的注意力分数后,加入两节点的边特征信息。

SignNet
问题:上述在使用Transformers处理图的过程中,使用拉普拉斯矩阵的特征向量作为位置编码。这么做有一个缺陷:由于特征向量具有符号不确定性(特征向量的方向无法确定,正负对称性),所以可能导致位置编码会出现不一致的情况,会严重影响模型的预测能力。
解决:可以使用一种通用的思想:SignNet用于解决符号不确定的问题。
设计目标:设计一个函数映射(神经网络)使得对不同符号的向量可以映射到同一个位置。(这个函数映射必须要有可表达能力)

- 显然,一个偶函数可以表达如下:
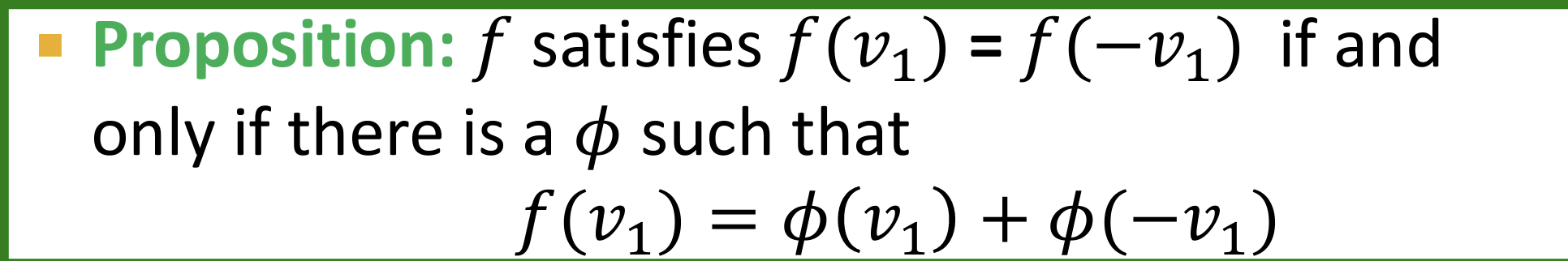
- SignNet核心思想如下:为了摆脱符号依赖,拆解偶函数。其中的$\phi$是一个公用的神经网络。

- 表达能力:SignNet can express all sign invariant functions!!
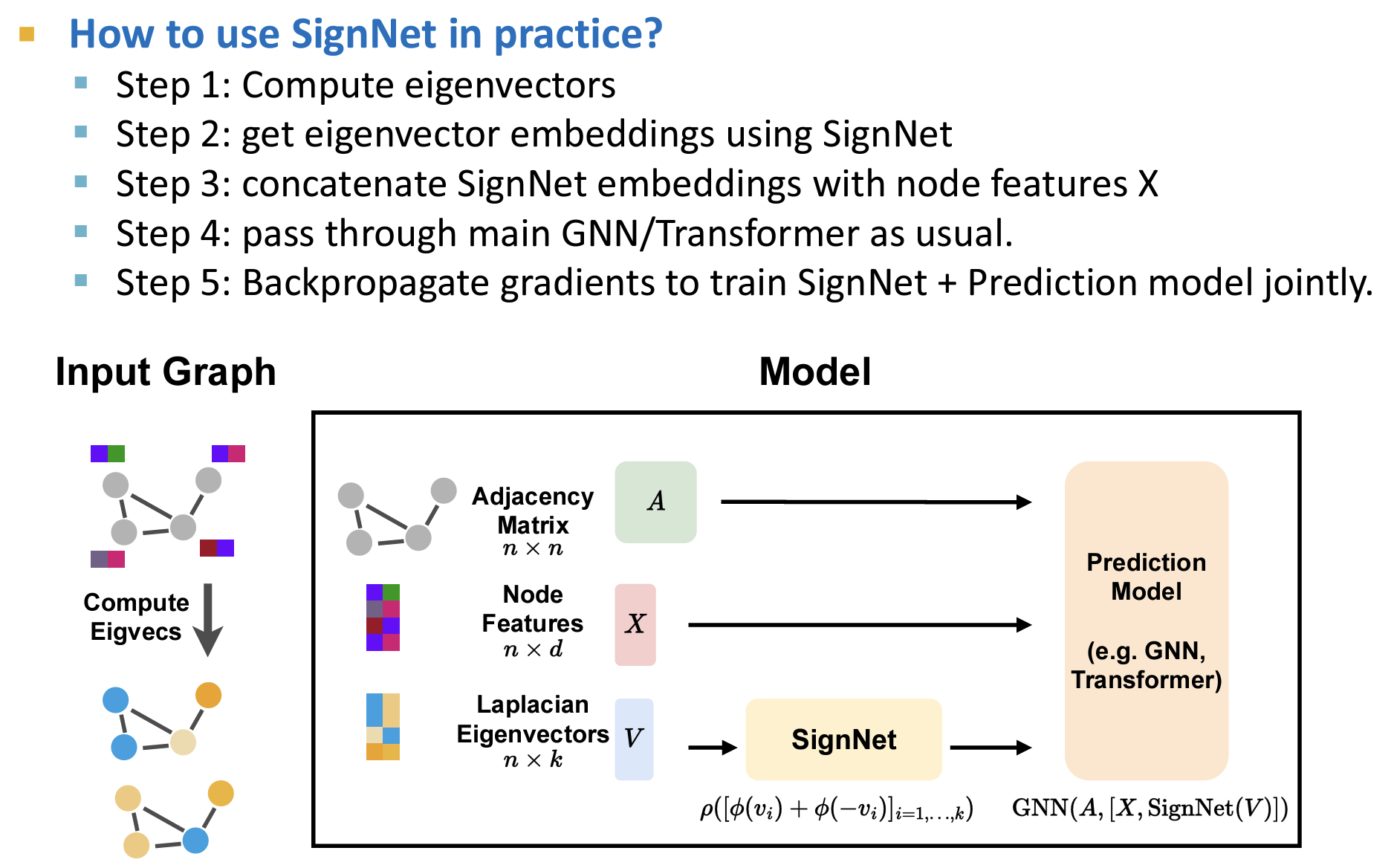
流程(使用SignNet)
- 位置编码使用:SignNet输出的符号无关的位置信息。
- SignNet参数和预测模型参数一同梯度回传和训练。
Day10
Scaling to large graphs

由于目前的应用(例如推荐系统、社交网络分析等等),图的规模巨大(10M-10B node/edge),需要考虑如何将GNNs适配到大规模的图上。
整图全批次(full-batch)训练
- 在第 $k$ 层,得到每个节点的embedding向量。
- 同时对所有节点进行更新(消息传递和聚合),得到第 $k+1$ 层的embedding向量。
- 但是不适用于大规模的图训练(GPU内存不足以存储整个图)
GPU内存不足?SubGraph Sampling子图采样
- 将大规模的图进行采样,使用子图存入GPU中用于训练。
- 如何采样(什么样的子图好)?should retain edge connectivity structure of the original graph as much as possible.【应该尽可能保持图中的边连接结构】
Cluster-GCN
- 核心思想:为了对整图进行采样,使用 group detection(例如节点聚类,分为一个一个的群体)的方法,将图分为一些列的节点簇,在它们上面分别进行训练。
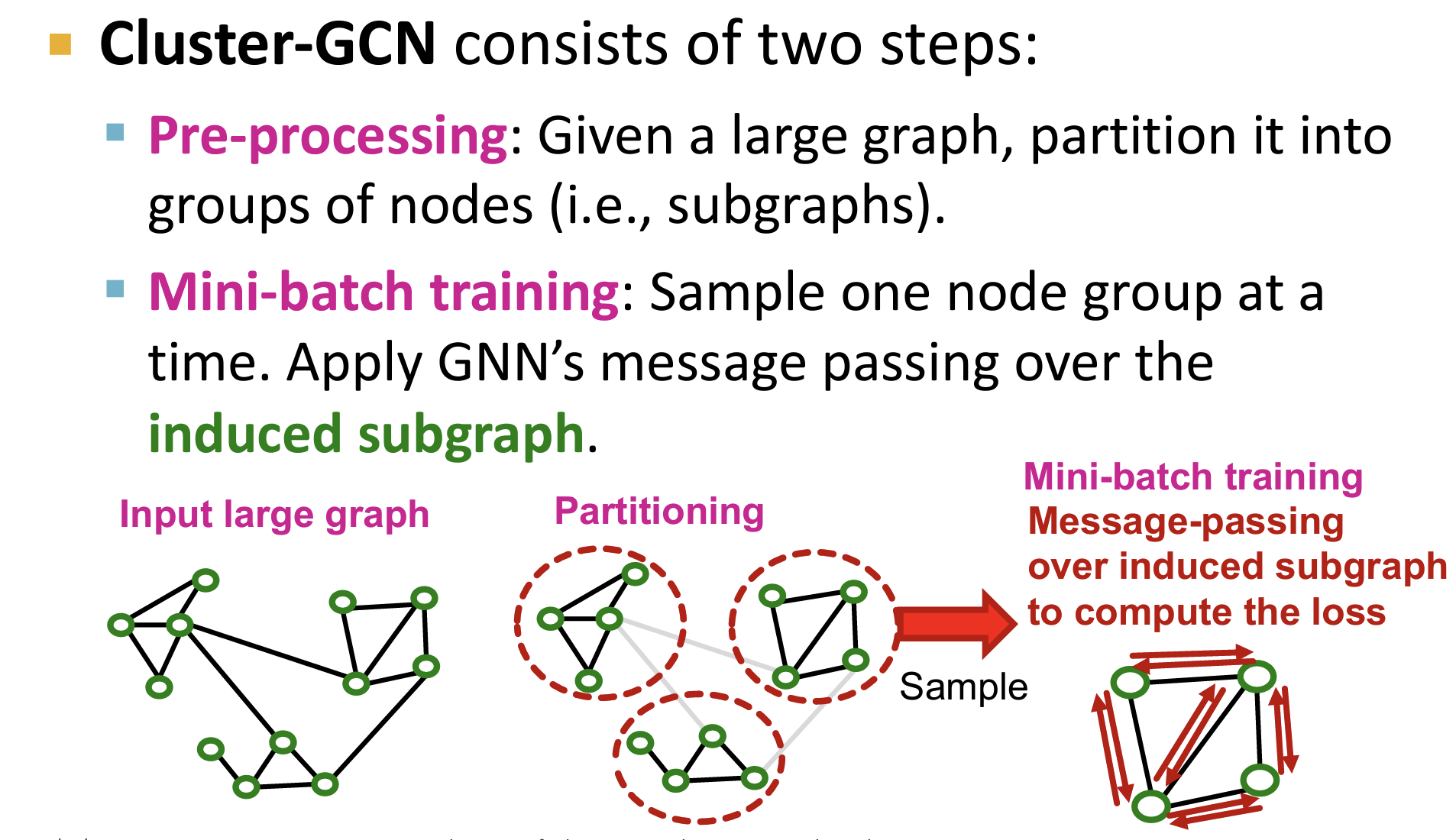
- Cluster-GCN在进行GNNs训练时,不考虑不同节点簇之间的连接关系。
- 有利于捕捉图的局部(group内)连接结构信息。
- 缺陷:
- 显然,无法捕捉groups之间的连接结构,损害 GNNs 性能。
- 由于子图的采样只涉及了图的一小部份节点和边,导致不同的group之间计算的梯度可能方差比较大,训练收敛比较慢。
通过简化 GNNs 的模型架构来增强其可扩展性
LightGCN
前文中提到过的LightGCN的主要思想就是去除节点特征的非线性变换来减少计算复杂度。这使得模型更加轻量级,适合处理大规模图数据。
通过邻接矩阵和度矩阵得到 正则后的邻接矩阵$\widetilde{A}$;通过初始的node embedding得到嵌入矩阵$E^{}$

- 普通 GCN 的矩阵计算形式(矩阵计算并行化程度高,加快计算速度)如下式所示。
$$
E^{(k+1)} = \text{ReLU}(\widetilde{A}E^{(k)}W^{(k)})
$$
- 其中的 正则邻接矩阵$\widetilde{A}$ 对嵌入矩阵 $E^{(k)}$进行扩散,权重矩阵$W^(k)$进行线性特征变换。ReLU进行非线性变换
- LightGCN 发现删除权重矩阵$W^(k)$ 几乎不会影响模型的性能。

即变为:
$$
E^{(k+1)} = \widetilde{A}E^{(k)}
$$所以LightGCN几乎只对节点的嵌入特征进行扩散(即相邻的节点趋向于拥有相似的嵌入特征)。
Day11 In-Context Learning Over Graph
上下文学习(ICL)
ICL,即In-Context Learning,是一种让大型语言模型(LLMs)通过少量标注样本在特定任务上进行学习的方法。这种方法的核心思想是,通过设计任务相关的指令形成提示模板,利用少量标注样本作为提示,引导模型在新的测试数据上生成预测结果。
- ICL主要思路是:给出少量的标注样本,设计任务相关的指令形成提示模板,用于指导待测试样本生成相应的结果。
- ICL的过程:并不涉及到梯度的更新,因为整个过程不属于fine-tuning范畴【预训练的大模型不需要进行微调,只需要根据提示,也就是上下文(in-context),就能够完成特定的任务。】。而是将一些带有标签的样本拼接起来,作为prompt的一部分,引导模型在新的测试数据输入上生成预测结果。
- ICL方法:表现大幅度超越了Zero-Shot-Learning,为少样本学习提供了新的研究思路。
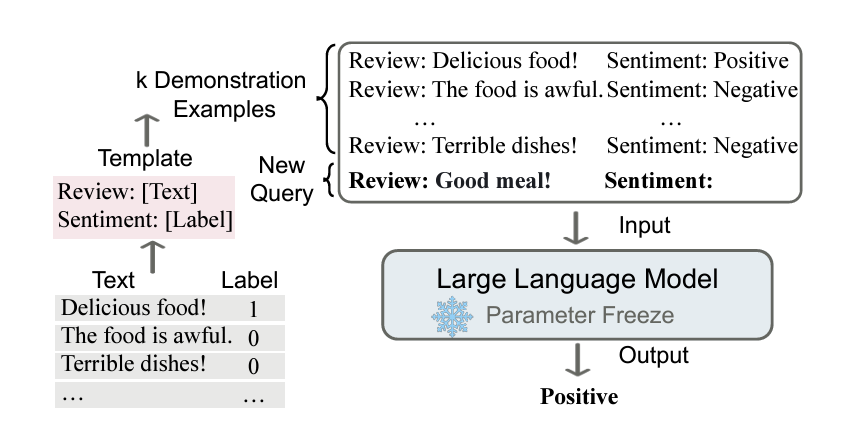
ICL需要一个包含一些用自然语言模板编写的演示示例的提示上下文。以这个提示和查询为输入,大型语言模型负责做出预测。
形式化定义如下:
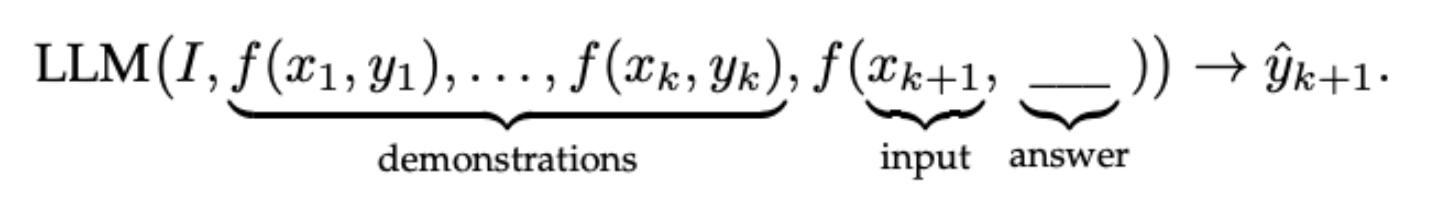
如下在Graph上进行ICL?
- 使用一个两阶段模型:

(1)构造Data Graphs:以Link Prediction为例,进行图采样选取prompt examples集合。
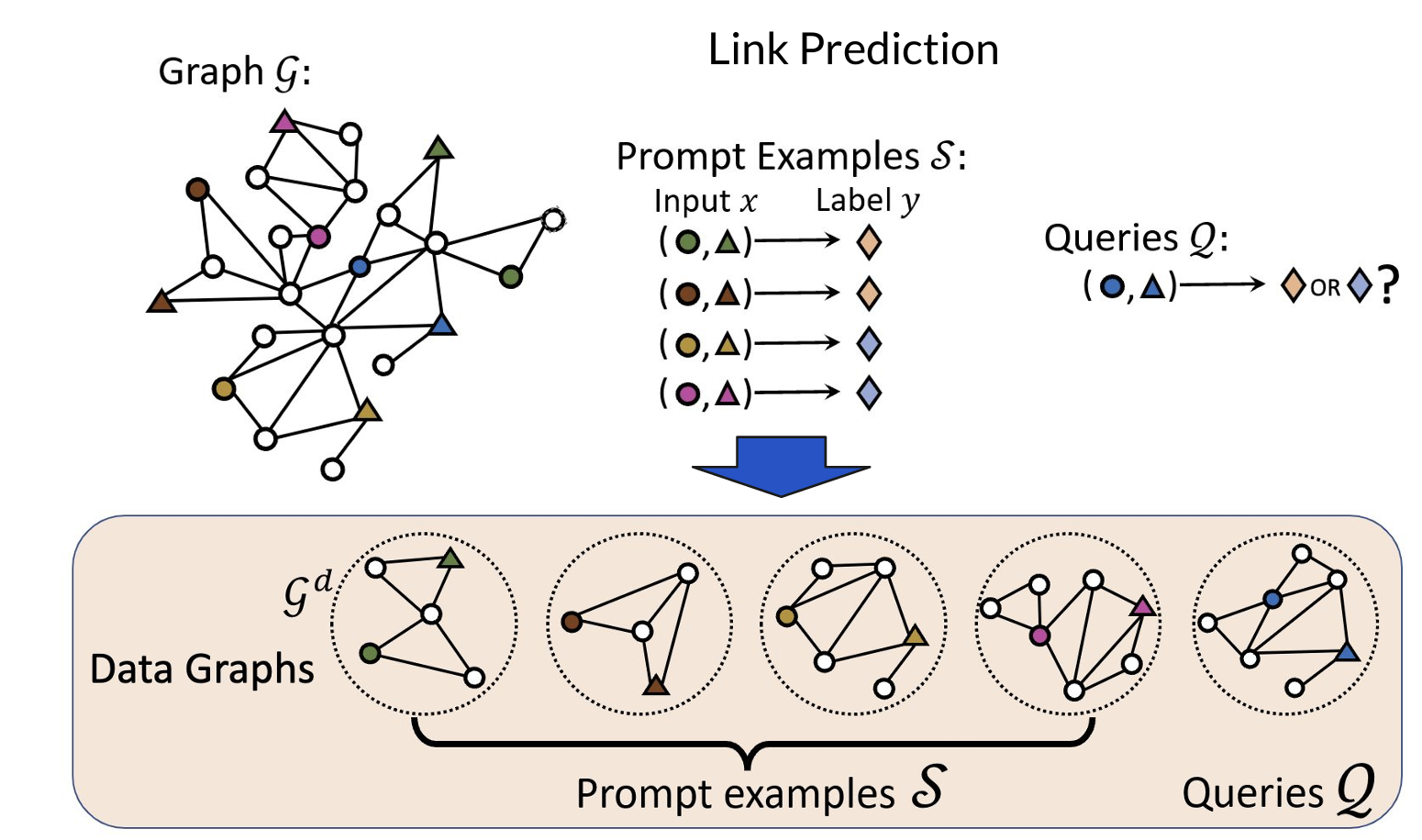
(2)构造Task Graphs:使用GNN对数据图进行encode
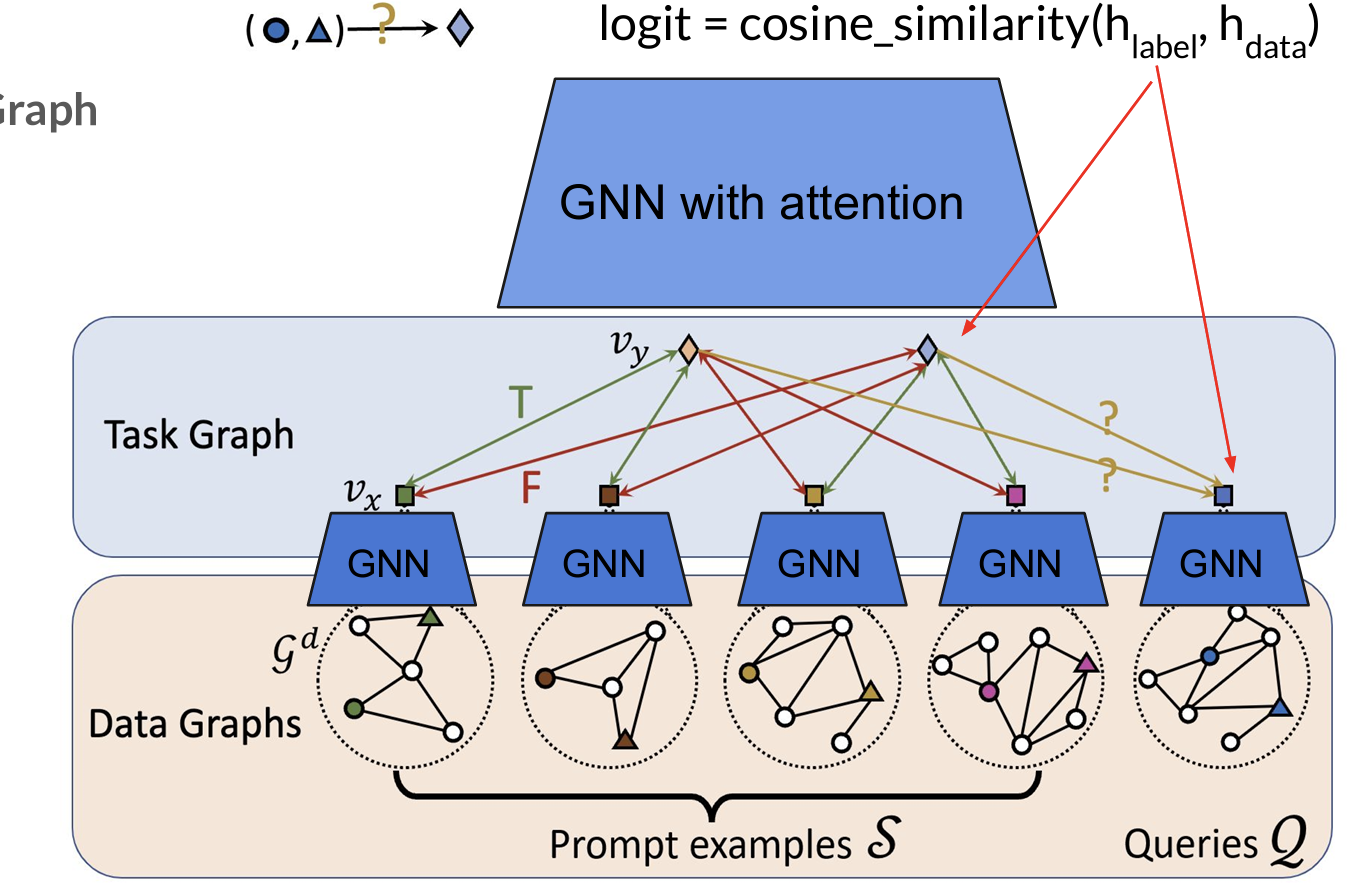
Day12 Algorithmic reasoning with GNNs

算法推理和GNNs
- 经典意义上的算法例如贪心、分值、递归等等,但是GNNs和这些经典算法的关系并不清晰。
- 探究:如何从算法的角度解释GNNs?它们之间的关系?GNNs架构和算法的关系和转换?
GNNs 和 1-WL 同构测试
简单回顾1-WL同构测试(用于图同构的判断,主要过程是:节点颜色初始化-使用邻居节点进行颜色哈希和传递-直到颜色稳定-读取图节点颜色直方图-判断图同构)
具体步骤
- 初始标记: 每个节点根据其初始属性(或没有属性时,所有节点赋予相同的初始标签)进行标记,通常使用单一的标签开始。
- 邻居聚合: 对于每个节点,将其当前标签与其邻居的标签集合进行组合,形成一个新的标签。例如,可以将节点的标签和所有邻居的标签进行排序,然后将排序后的标签连接在一起。
- 标签压缩: 将每个节点的组合标签映射到一个新的紧凑标签(例如通过哈希函数)。这一过程通常称为“标签压缩”。
- 重复迭代: 对整个图重复步骤2和步骤3若干次。在每次迭代中,节点的标签会越来越复杂,越来越能反映其在图中的结构位置。
- 比较标签分布: 在经过若干次迭代后,比较两个图中所有节点的标签分布。如果在某次迭代后,两个图的标签分布不同,则可以断定这两个图不可能是同构的。
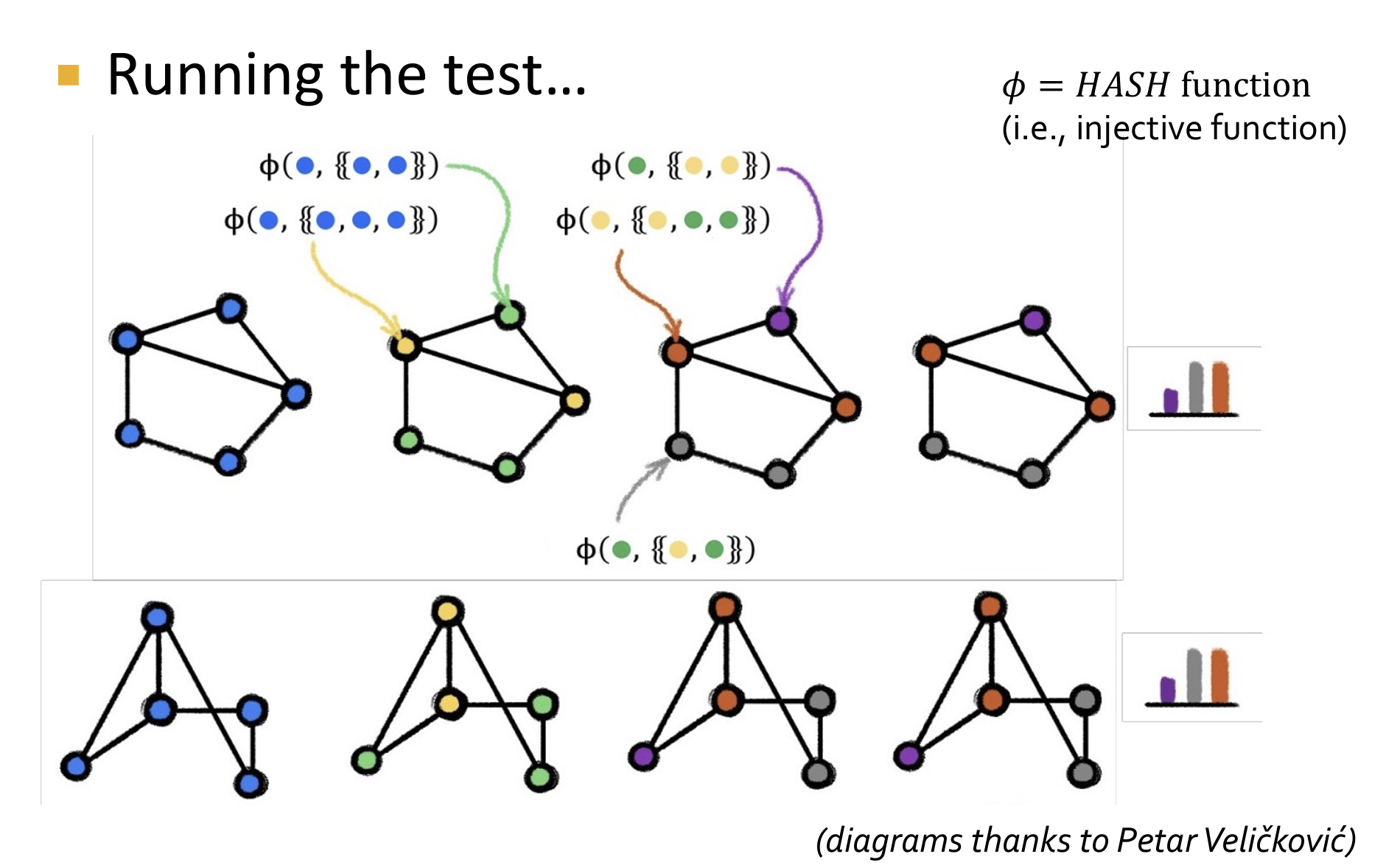
- GIN(Graph Isomorphism Network) is as expressive as the 1-WL test
- GIN Replaces HASH function with learnable MLP (将1-WL测试的哈希函数替换为了可学习的MLP)
- GIN is a “neural version” of the 1-WL algorithm
- 这证明了:GNNs 模拟了一些经典算法的实现
- 事实上:An untrained GNN (random MLP = random hash) is close to the 1-WL test【GNNs的参数初始化时相当于一个随机哈希函数】
神经网络作为算法
- 这一节讨论的不是神经网络的表达能力(expressive power),而是其在少数据样本下的能力。

- MLPs 可以轻松【easily,在少数据下】模拟一些smooth functions(例如线性、log函数等);但是对于相对复杂的函数,例如求和、for循环等,需要大数据样本的学习才能进行模拟。
特征抽取问题:MLP可以轻松模拟
- 即从多个输入中选取特征(类似于一个线性函数),MLP可以轻松模拟

对于概要统计问题:MLP无法轻松模拟
- 例如求坐标最大值,相当于一个for-loop求解最大值的算法,MLP无法直接进行模拟。
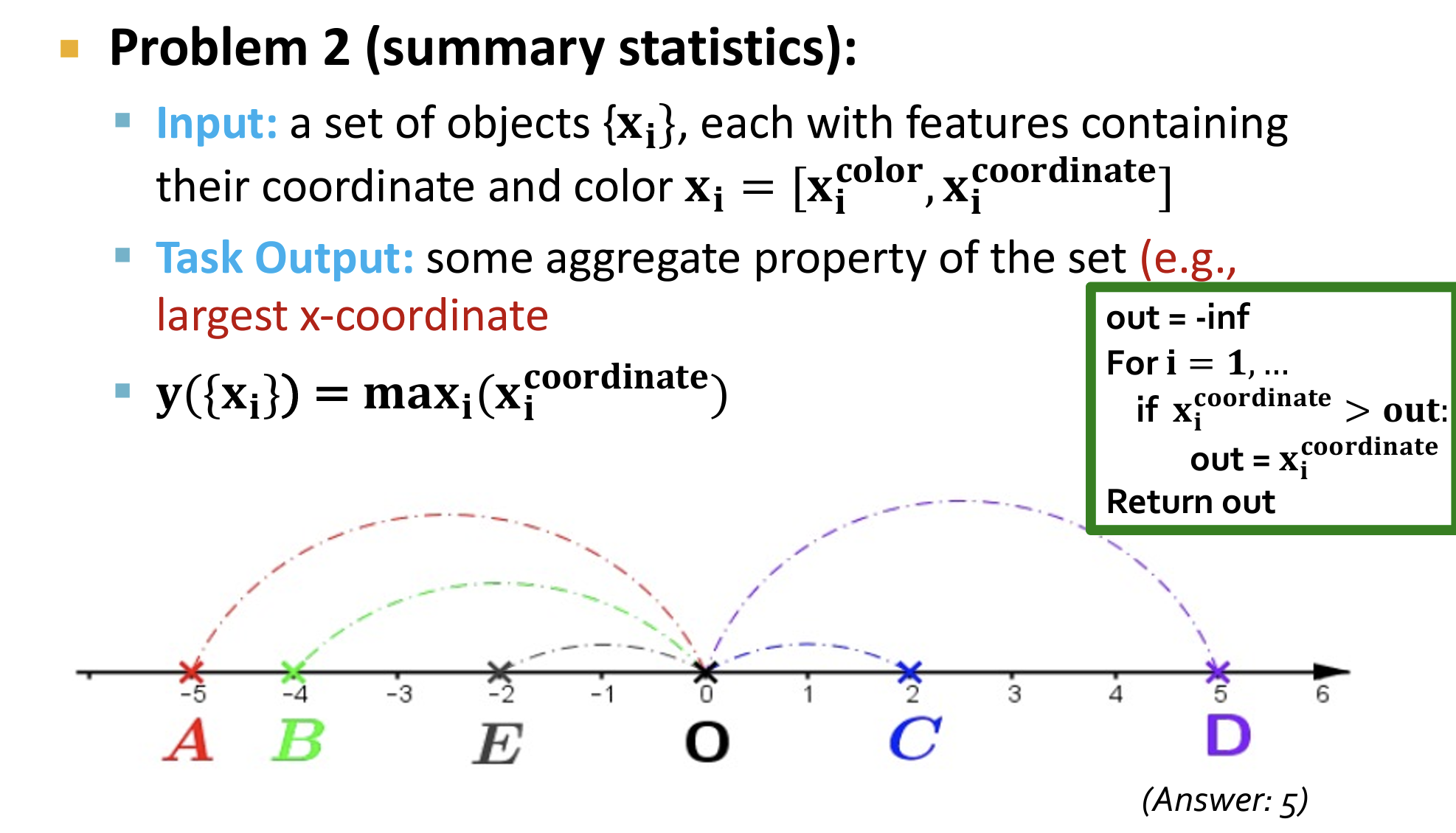
转换:使用嵌套MLP
- 最大值函数可以通过对数和指数函数来近似表示(通过指数函数来放大差异,从而使得输出只由最大的$x_i$决定)

- 其中的对数函数和指数函数都可以使用MLP模拟,建立DeepSet模型:
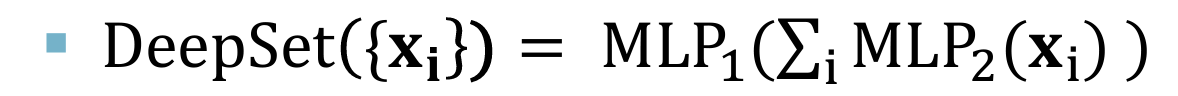
Relational Argmax问题
- 更加复杂的pairwise问题,找到距离最远的两个坐标
- 相当于一个两个for-loop嵌套的问题:对于每一个点,使用一个for- loop找到最远点;对于所有点的最远距离,使用一个for-loop找到最大值。

- DeepSet无法解决两个for-loop嵌套的问题。
使用GNNs:

总结

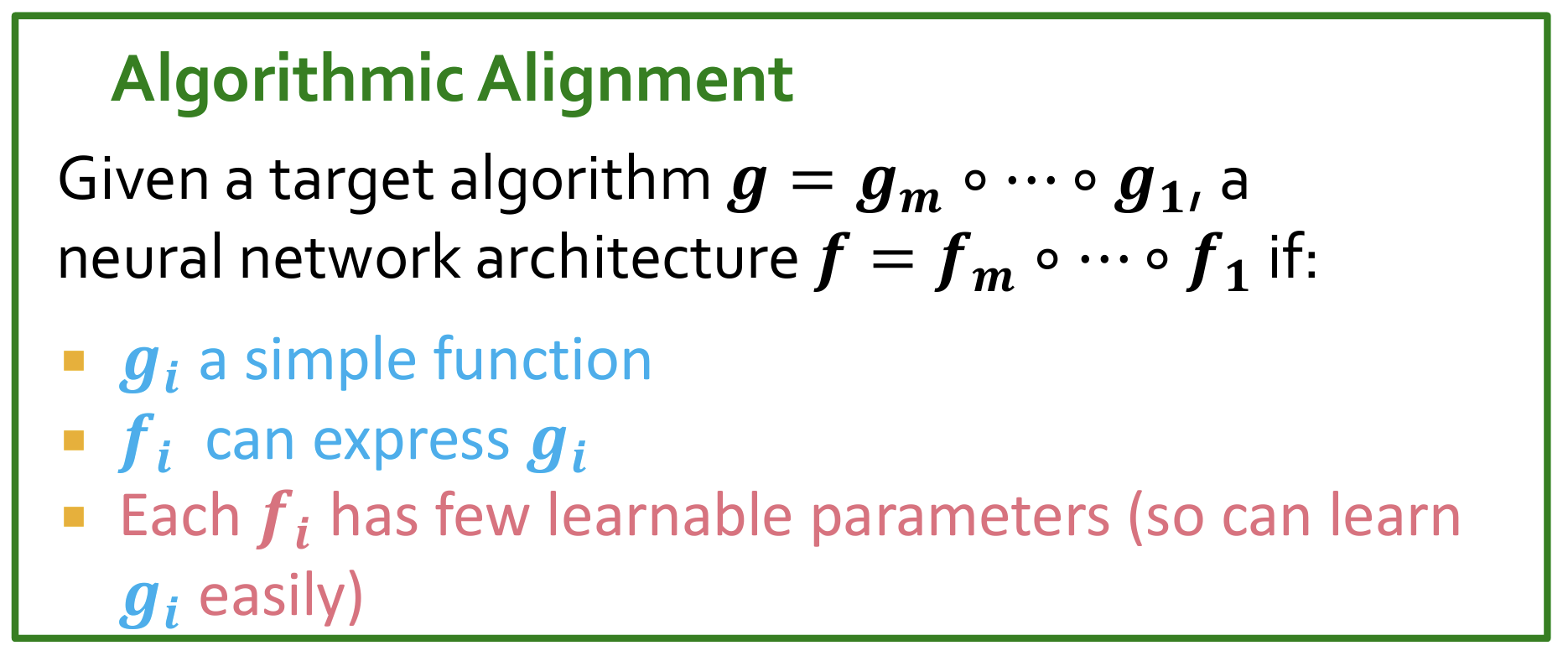
重点:Algorithmic Alignment
- 在使用一个NN结构模拟目标算法时,或者使用算法来公式化一个NN架构时,使用如下的等价方法。
Day13
GNNs Design space
- GNNs(Graph Neural Networks)的Design space指的是设计和构建GNN模型时的可选组件和方法的范围或集合。这个空间包括了不同的设计选择、架构模块和操作,它们共同决定了GNN的表现和适用性。Design space的探索旨在优化GNN模型以更好地适应不同类型的图数据和任务需求。
- 对于不同的任务,不同的GNNs性能不同。没有一个通用的SOTA模型可以适用于所有图任务。
GNNs Task Space
如何将GNN适用的任务进行分类?如果仅仅按照node/link/graph level进行分类,精确性太差。
如何定义可以量化的图任务相似度的指标?作用:可以用于对不同的图任务快速挑选合适的GNNs模型;否则很困难。

锚点模型
- 挑选固定的锚定模型,作为不同任务的特征之一进行排序和相似性计算。
- 思考:例如对于任务A和任务B都属于node classification任务,但是不清楚其相似性。可以使用挑选出的锚点模型进行判断。
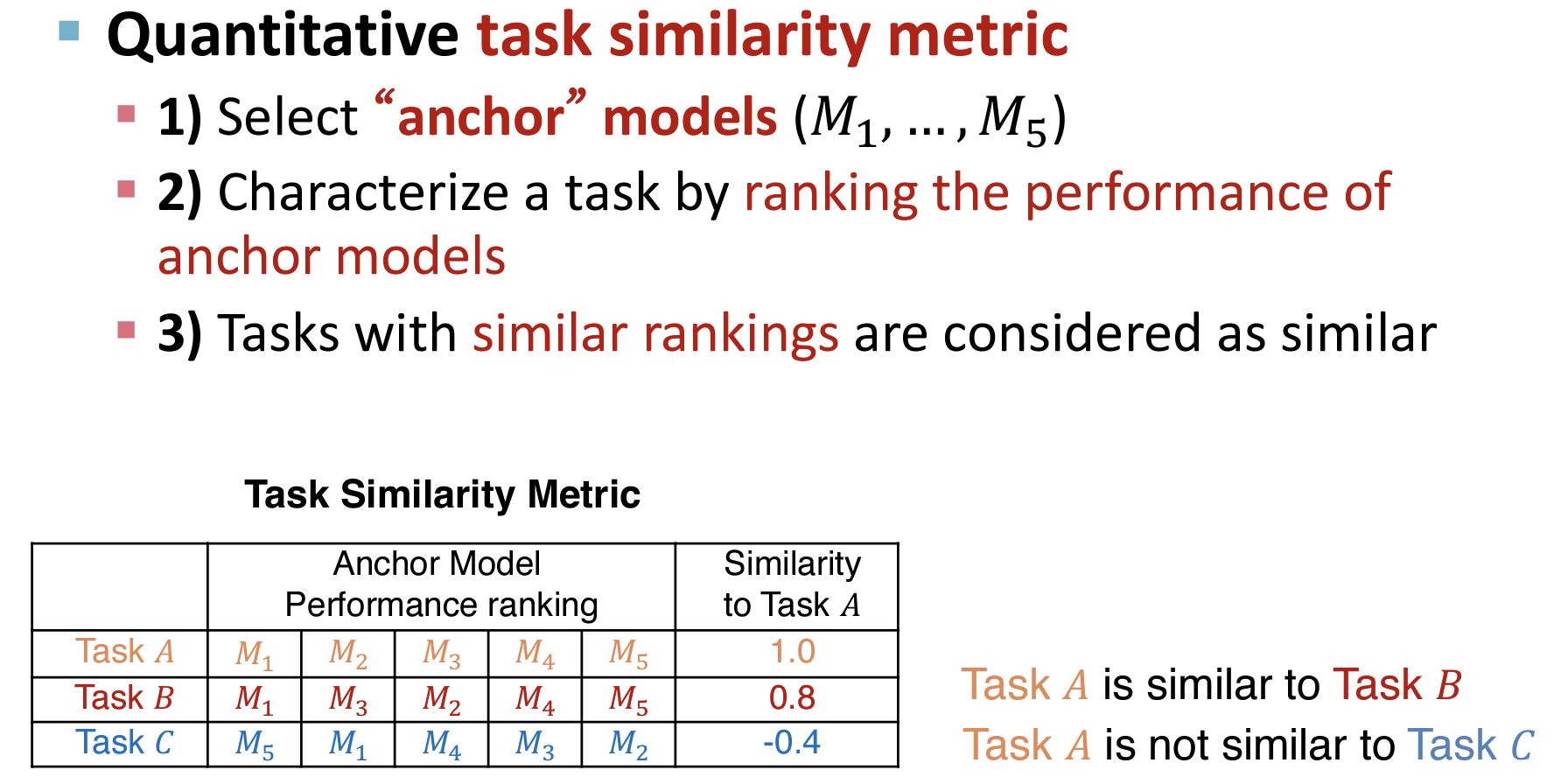
- 如何挑选这些“Anchor”模型?直觉是:Anchor模型必须具有良好的表征性和多样性。
- 可以通过给定一个小的数据机,随机采样N个模型训练并性能排序,最后选择性能广度较大的M个模型。(目的是尽可能包含性能好的和性能差的模型)

- 在新的task进入时,使用锚定模型计算性能,并通过和其它tasks计算相似度,从而推荐相似任务的最优模型给新启动的task。(类似于推荐系统的冷启动)
如何评估GNNs的Design?
- 随机采样 任务-模型对【task-model pair】,在这些pairs中进行消融分析(例如对于BN,分别训练含有BN和不含有BN,对其结果进行统计和评估。
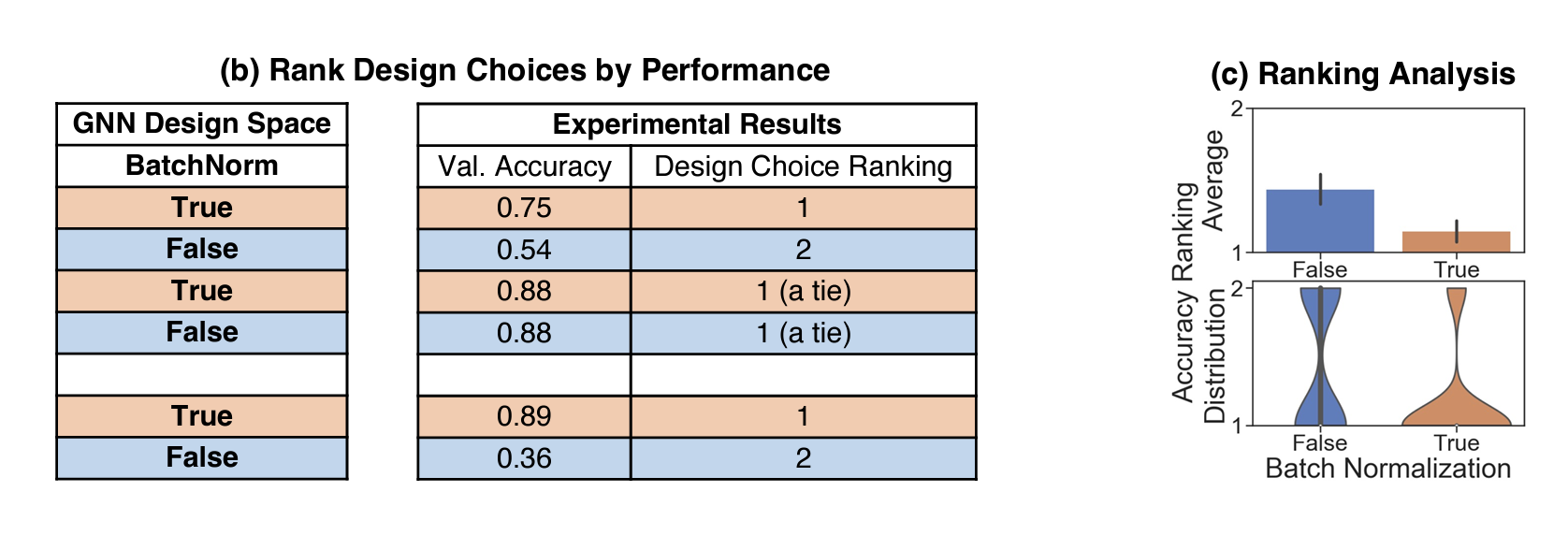
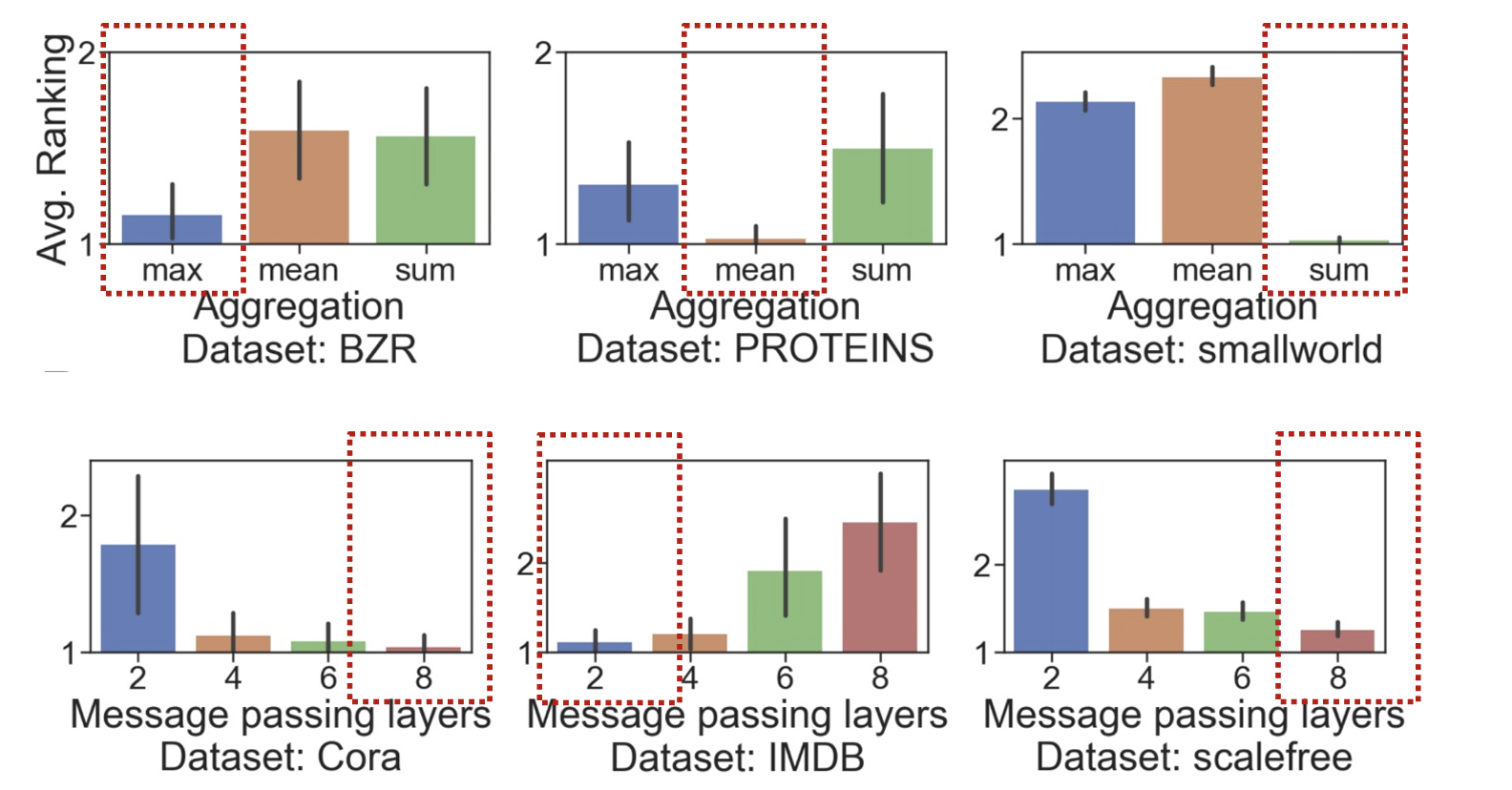
- 可能对于不同的任务和数据集,使用不同的Design具有不同的性能。
——————————————————🌹🌹🌹🌹🌹🌹 END 🌹🌹🌹🌹🌹🌹🌹————————————————————
