CS-246[大数据挖掘]

Lee

2024-08-22

大数据, 数据挖掘

CS246: Mining Massive Data Sets

大数据挖掘

课程网站：CS246: Mining Massive Data Sets Winter 2024
概要：用于分析大数据[Massive Data]的数据挖掘和机器学习算法。
课程版本：24Winter 学习时间：24Fall
本博客记录自己的学习过程以及用于复习和回顾。

课程重点将放在MapReduce和Spark作为创建可以处理大量数据的并行算法的工具。
主题包括：频繁项目集和关联规则、高维数据中的近邻搜索、局部敏感散列（LSH）、维度减少、推荐系统、聚类、链接分析、大规模监督机器学习、数据流、结构化数据挖掘网络、网络广告。

Section0：Intruduction

本课程主要涉及数据挖掘，即对数据的分析；绝大多数涉及机器学习技术

主要课程内容可以划分为几个模块：

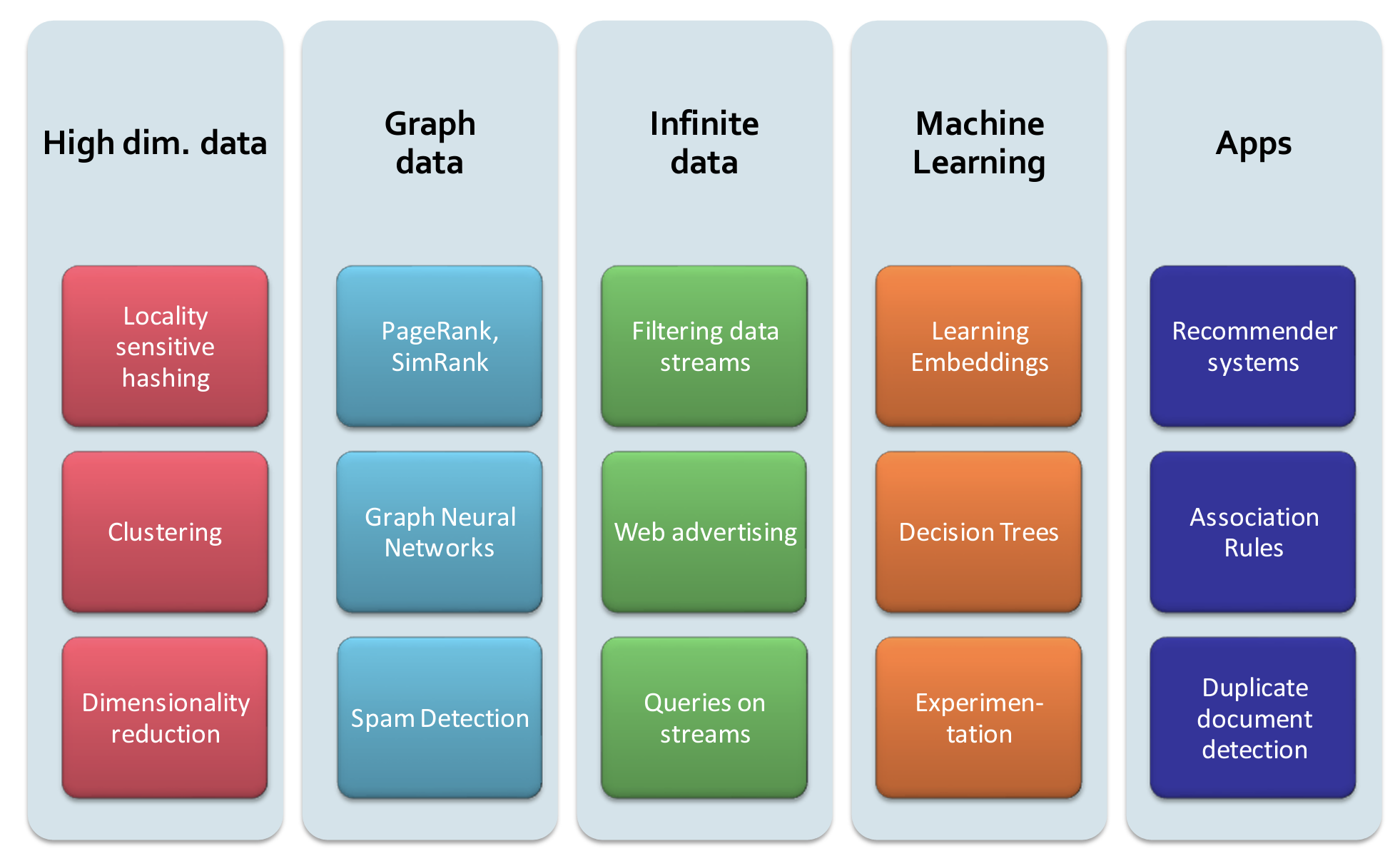
Section1： MapReduce and Spark

分布式计算

解决大规模数据计算的问题
在不同的节点进行数据的存储和计算
数据存储：分布式文件系统（GFS【Google】、HDFS【Hadoop】）
分布式计算模型：MapReduce、Spark

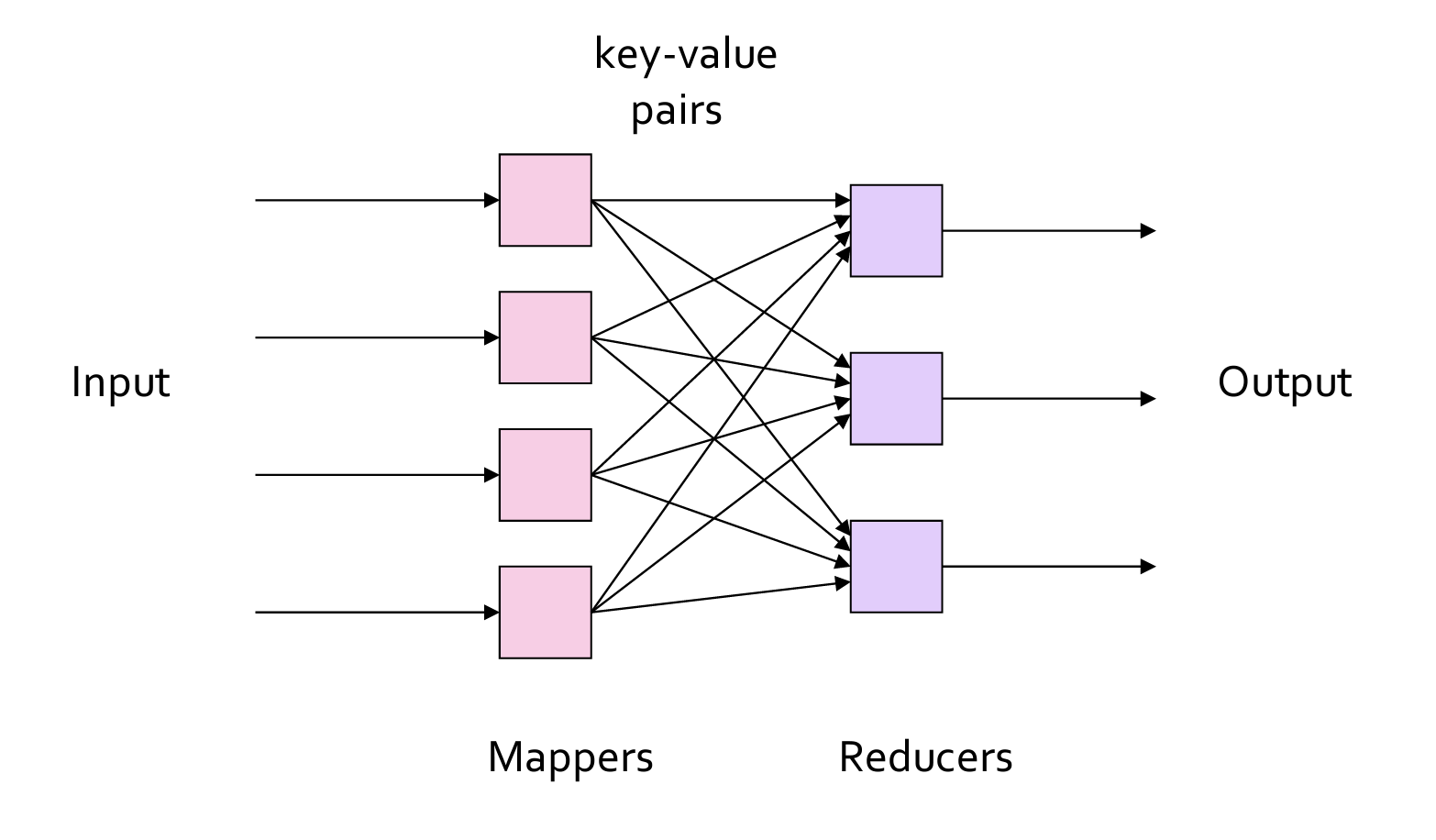
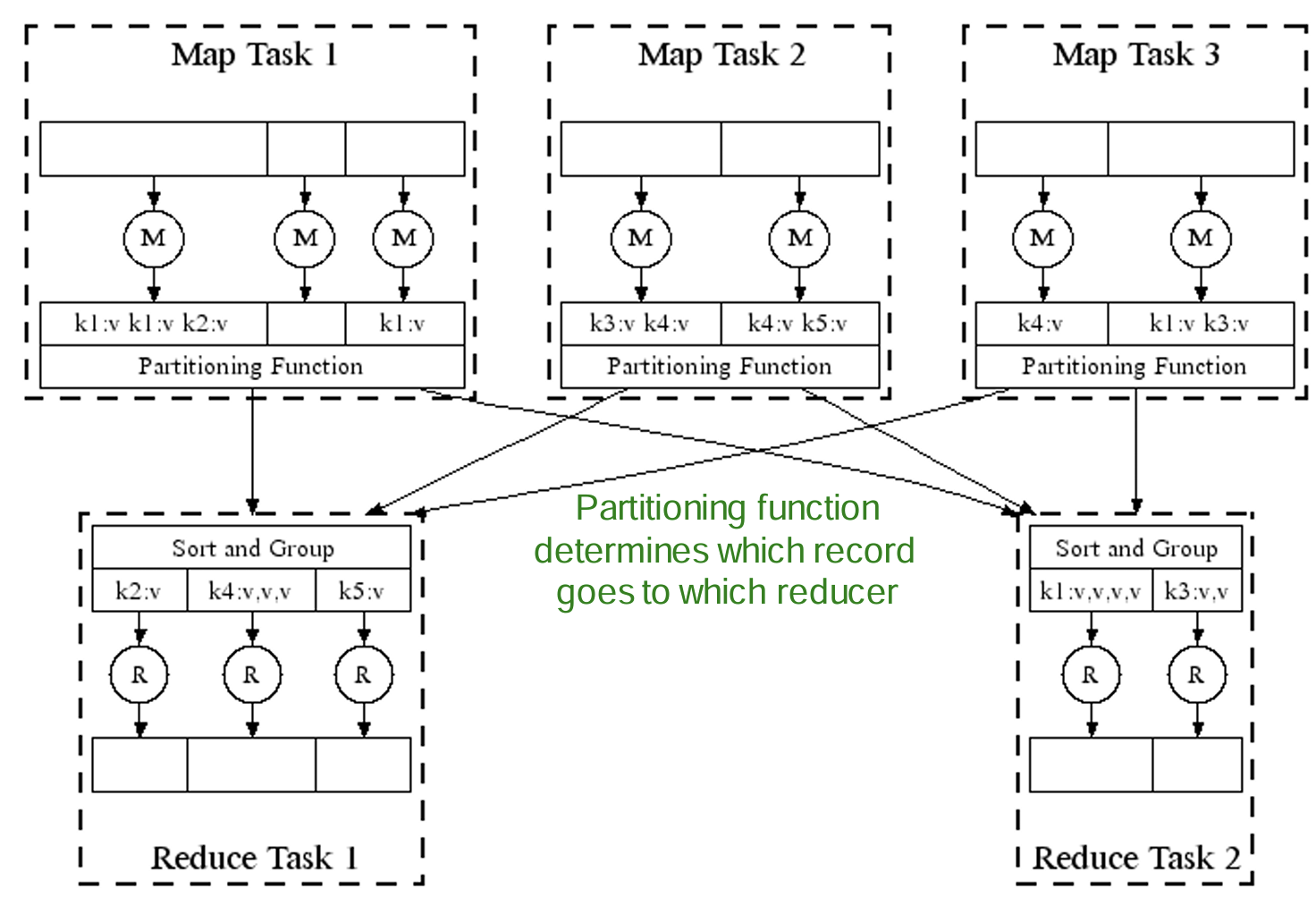
MapReduce

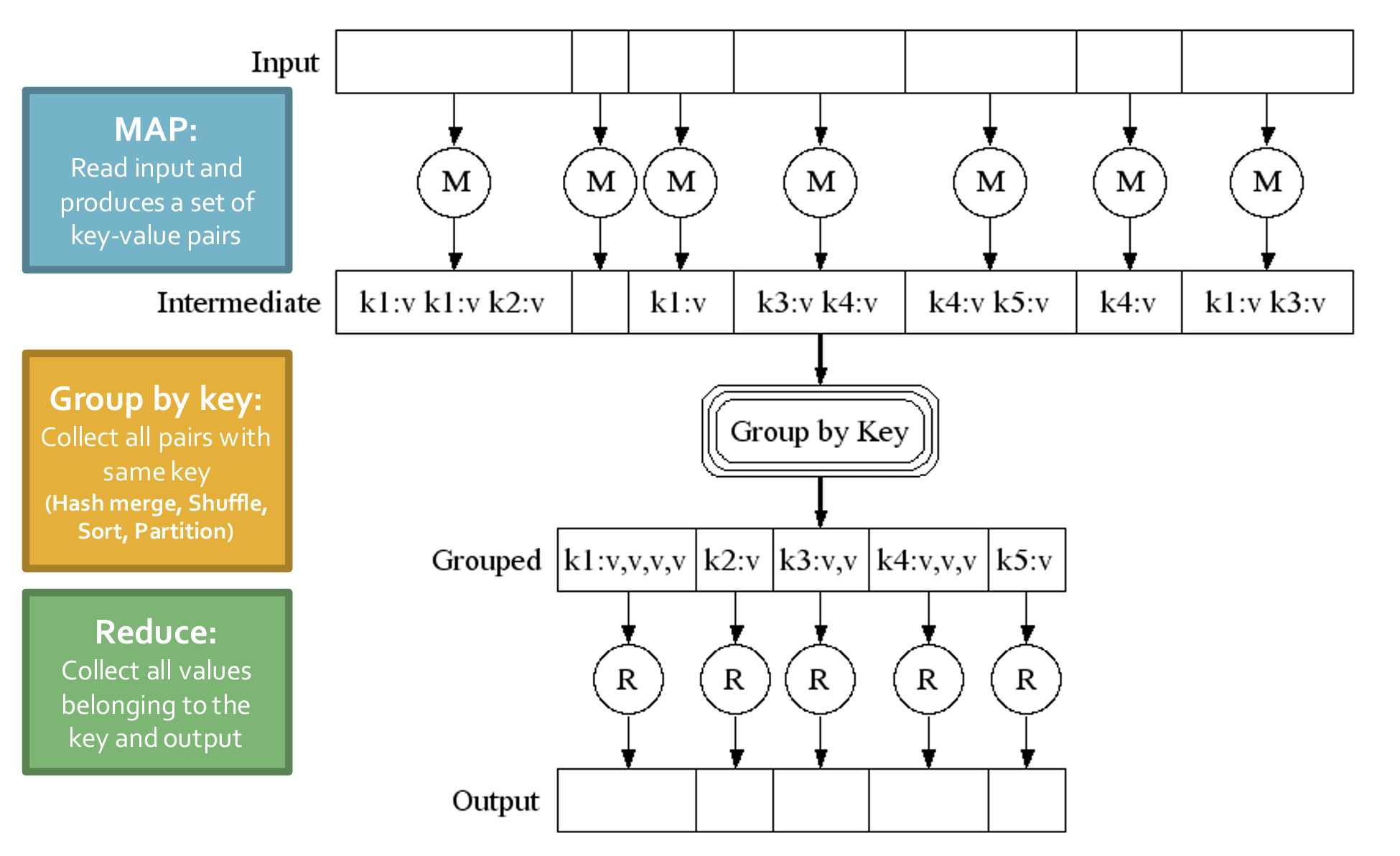
主要的三个步骤：Map、Group by key、Reduce、
Map：对每一个Item/entry 使用Mapper进行映射为一个 key-value pair，键值对的含义具体由应用制定；
Group by key：使用key对所有键值对进行排序；
Reduce：对同一个Group内的键值对进行规约操作。

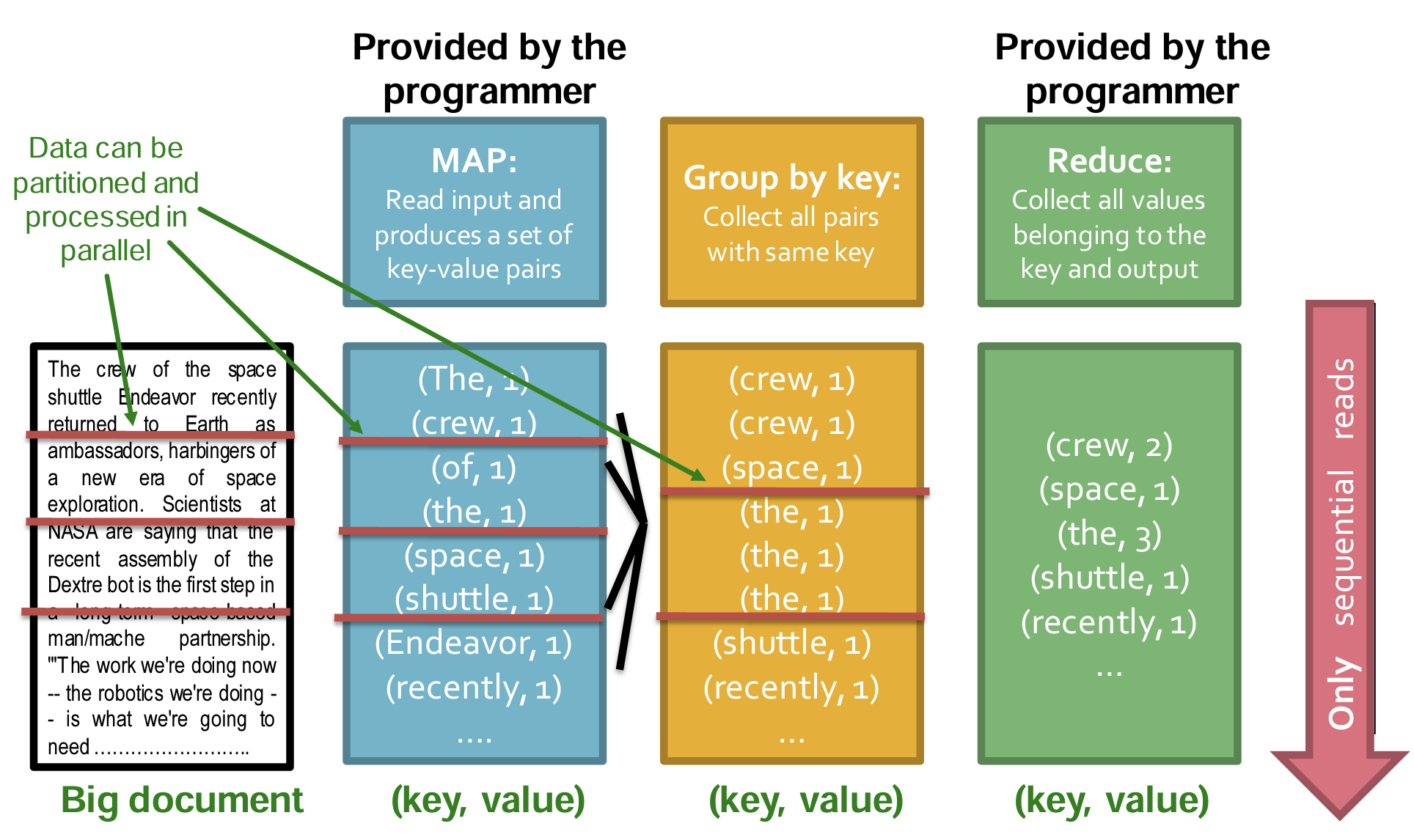
例子：词频统计（将词汇作为key，词频作为value；Group by key将相同词排序在一起；Reduce进行合并）

MR过程如何进行分布式多机计算？并行进行Map后，在Group阶段每台机器收集各自的pair进行规约。

Spark：对MapReduce的扩展

MapReduce存在什么问题：
- 性能瓶颈：为了节约内存，使用硬盘[以及文件系统]进行存储和读写，由于数据复制、磁盘I/O和序列化，MapReduce会产生大量开销（Mapper从disk读进行映射，写回disk；然后Reducer又要从disk读取进行规约，再写回）
- 运用困难：Map-Reduce的逻辑有时无法运用到一些大数据计算的任务中；（强编程范式，比较死板）
Spark内存计算，速度性能由于MR；Spark支持除了Map和Reduce更多高阶操作；Spark开发难度低（高阶API）
什么是Spark？四个主要接口

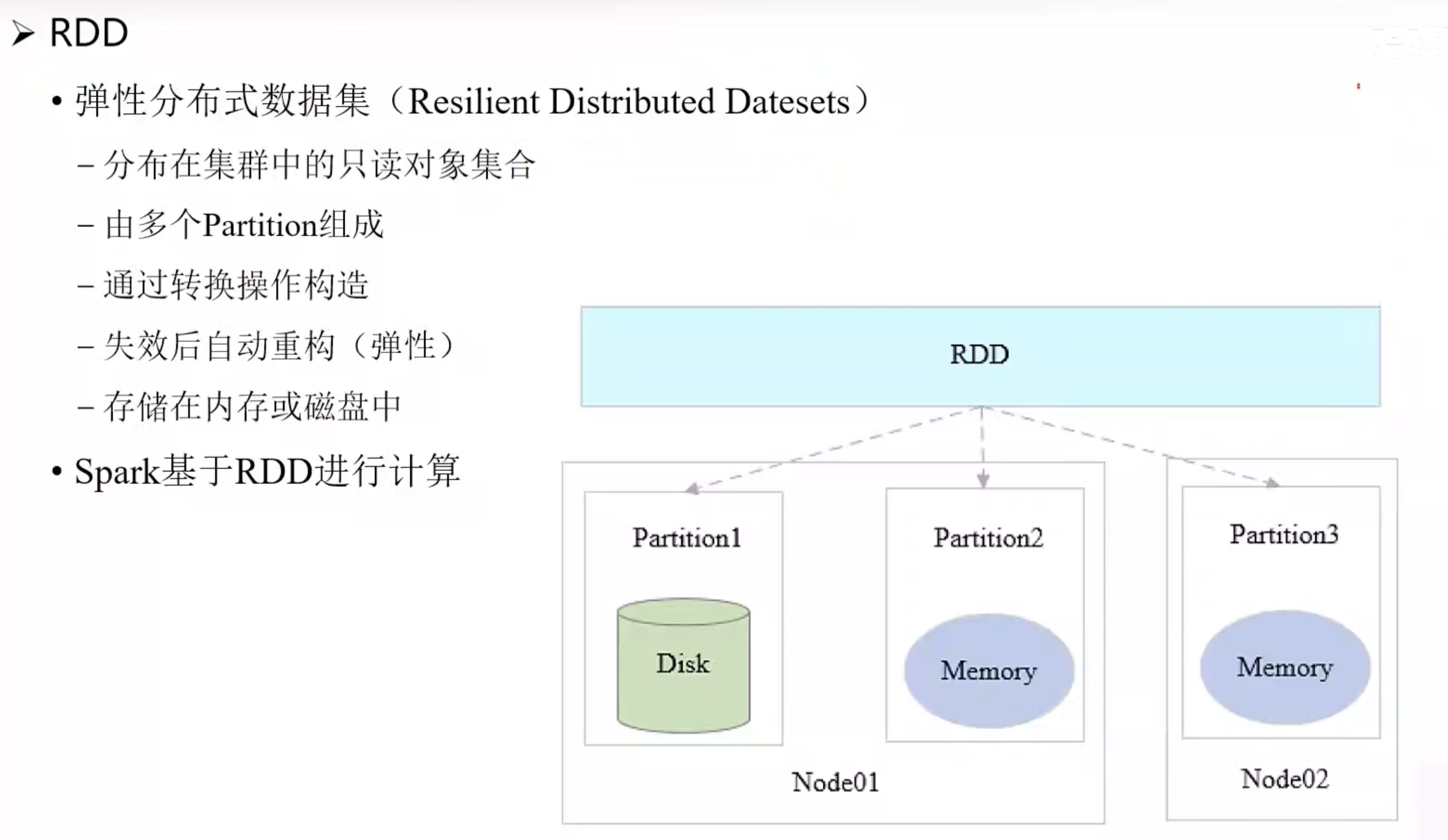
核心数据结构： Resilient Distributed Dataset (RDD) 弹性分布式数据集
- 什么是弹性？什么是分布式？

Spark使用Scala语言开发，支持其他例如 Java/Python 等语言。
例如：RDD in 词频统计

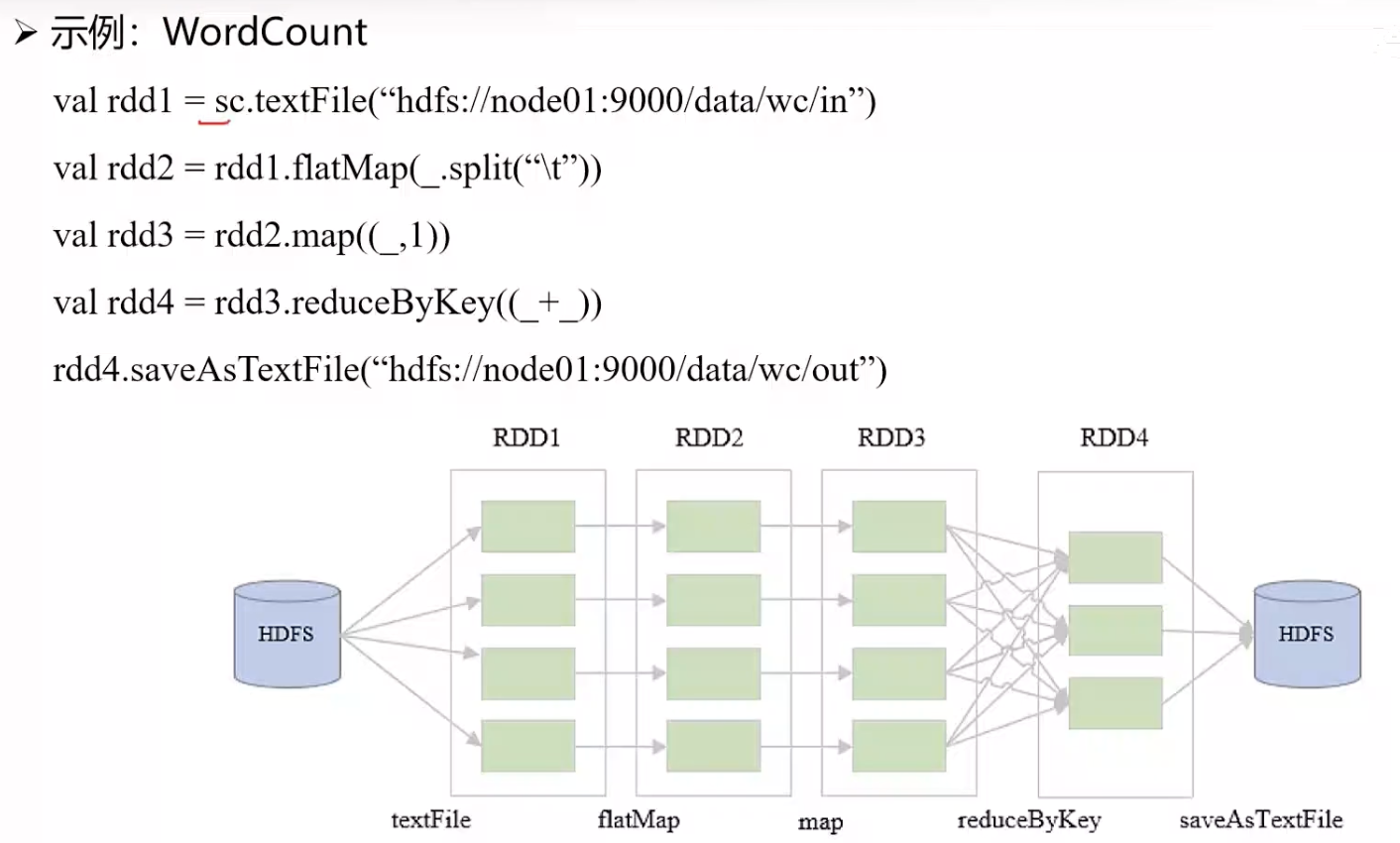
如上所示，可以看到Spark的 RDD的数据流是一个DAG（有向无环图）。
- 有利于数据恢复（当某一计算节点失效只需回复到上一阶段，而无需重新从头开始），这就是弹性。
RDD支持两种操作：Transformations 以及 Actions

MapReduce应用

数据库表连接操作：

Section2：Frequent Itemsets Mining & Association Rule

频繁项集挖掘和关联规则

概念解析：

Items and baskets 是数据挖掘中一个常见的概念，尤其是在市场篮分析（Market Basket Analysis）中。这些术语通常用于描述消费者购买行为或其他事务性数据。以下是这些概念的详细解释：

1. Items（项目）

定义: 项目（Items）指的是单个的产品、商品或对象。在市场篮分析中，项目可以是任何可以被购买或交易的东西。例如，在超市里，一个项目可以是牛奶、面包、鸡蛋等商品。

例子

在电子商务网站中，项目可以是用户可以购买的各种商品，如手机、书籍、衣服等。

在音乐流媒体服务中，项目可以是不同的歌曲、专辑或艺术家。

2. Baskets（篮子）

定义: 篮子（Baskets）是指一组项目的集合，通常表示一次交易或购买行为。在市场篮分析中，每个篮子代表一位顾客在一次购物中所购买的所有项目。

例子

在超市购物中，篮子可以表示一个顾客在一次购物中购买的所有商品，如 {牛奶, 面包, 鸡蛋}。

在在线购物中，篮子可能表示用户在一次交易中购买的所有物品，如 {手机, 充电器, 耳机}。

在图书馆的借阅记录中，篮子可以表示一个读者一次借阅的所有书籍。

市场篮分析（Market Basket Analysis）: 通过分析顾客的购物篮（baskets），发现哪些项目（items）经常一起购买。例如，超市可能会发现牛奶和面包经常一起被购买，于是可以在促销活动中捆绑销售这些商品。

Items 和 Baskets 都是抽象的，在不同的应用场景中有不同的含义。

Frequent Itemsets Mining

频繁项集是指在交易数据库中频繁出现的一组项目。简单来说，频繁项集是那些在多个事务中共同出现的项目组合。
一个项目集的频繁程度通常通过它的支持度（Support）来衡量。支持度指的是在所有交易中，包含某个项集的交易所占的比例（或者绝对数量）。
频繁项集挖掘的目标是找到所有的项集，这些项集的支持度至少达到预先定义的最小支持度阈值（Minimum Support Threshold）。

Association Rule

关联规则用于揭示频繁项集之间的强关联关系，通常表示为$A \Rightarrow B$，意思是“如果 A 发生，那么 B 也很可能发生”。
关联规则由两部分组成：前件（Antecedent，A）和后件（Consequent，B），它们都是频繁项集。

评价指标

支持度（Support）: 一个规则的支持度是前件和后件共同出现的概率。它表示了整个数据库中该规则适用的程度。
$\text{Support}(A \Rightarrow B) = P(A \cup B)$
置信度（Confidence）: 置信度衡量了在前件发生的情况下，后件发生的概率。
$ \text{Confidence}(A \Rightarrow B) = P(B|A) = \frac{\text{Support}(A \cup B)}{\text{Support}(A)} $
存在什么问题？当$P(B)$较大时，置信度虽然很高，但是没有实际意义。

解决：兴趣度（Interest）
$Interest(I→j)=conf(I→j)−P(j)=∣P(j∣I)−P(j)∣$

兴趣度使用绝对值的意义在于判断其正相关关系或者是负相关关系。

如何找到关联规则？

如下是一个例子：

定义阈值信息。
首先找到所有的频繁项集（这里可以筛选掉一些非最大化的频繁项，具体的方法之后详细给出）
根据如下式子，进行关联规则的生成。（在每一个频繁项中，挑选其子集进行判断和生成）

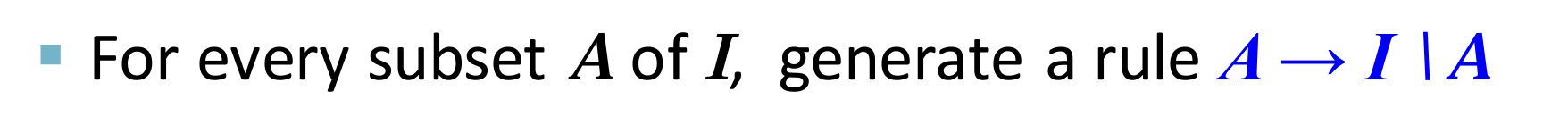
Step2 中需要找到所有的频繁项集，如何实现？
- 朴素的暴力算法实现的话，以寻找两个item大小的频繁子集问题为例，需要两次循环遍历计算每一个pair的出现次数。
- 当 Baskets 的items的数量过大，内存无法容下。（内存问题）

A-priori 算法

基于一个思想：即如果一个item的出现次数都没有超过阈值，那么不可能有频繁项集包含该item。
所有的出现次数超过阈值的单个item称为frequent item，任何频繁项集只能由这些freq. item组成。
算法流程：逐步的过滤和构造

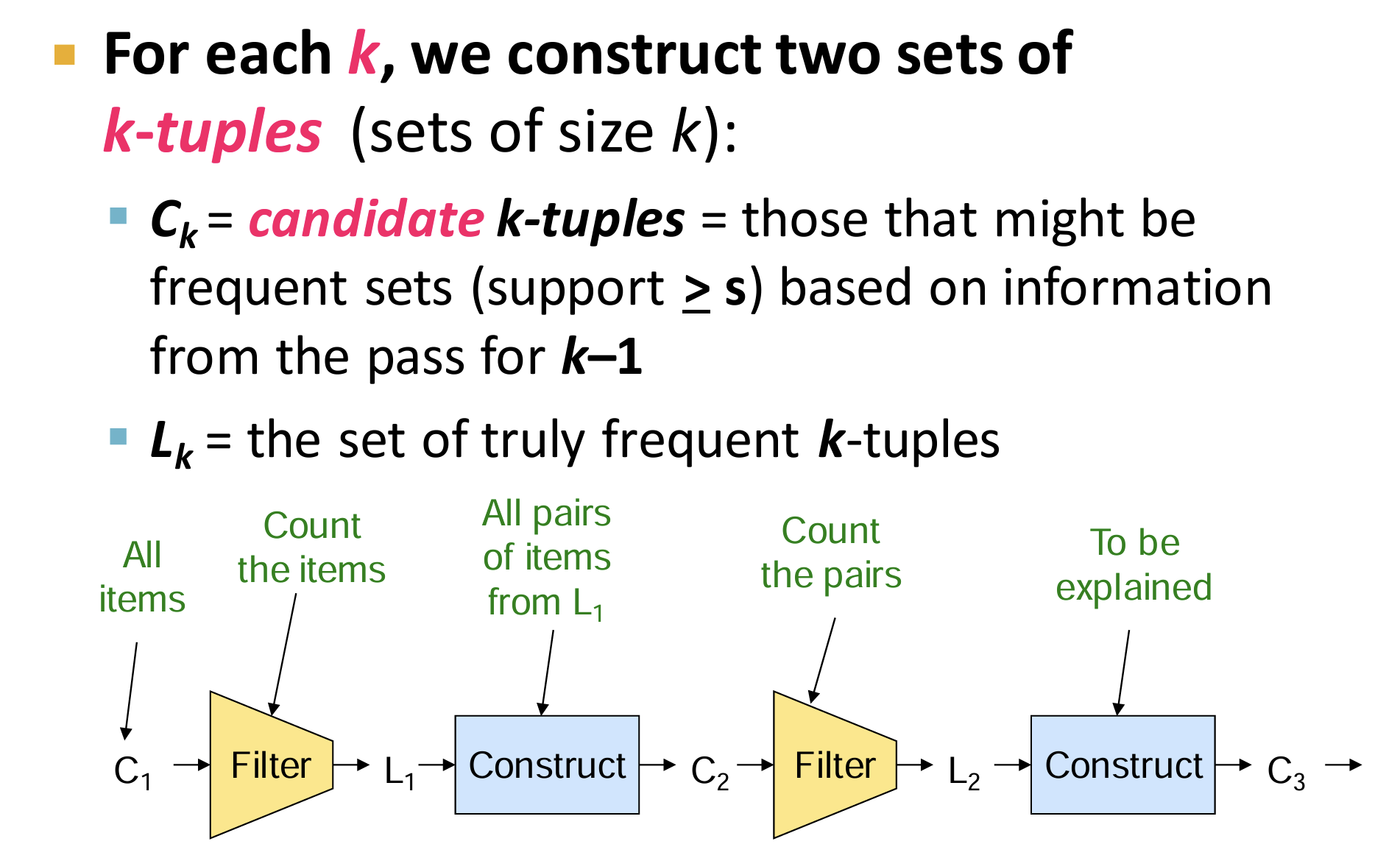
从freq. item（size=1），逐渐构造更大size的item set；

Section3: Locality-Sensitive Hashing

一种最近邻算法
局部敏感哈希，一种用于高维数据的近似最近邻搜索的技术。
主要目标：将高维空间中的相似数据点映射到同一个桶（bucket）中，以便快速发现相似的项。

文档相似性检测

如下图所示，文档相似性检测是一个经典的任务；在文档数量极大的前提下，如果两两比较开销巨大。

如何定义文档之间的相似性？

将文档视为一个集合，定义集合之间的相似度使用 Jaccard similarity

进行文档相似性检测的三个典型的步骤和模型图如下图所示（其中第三步使用了LSH）。

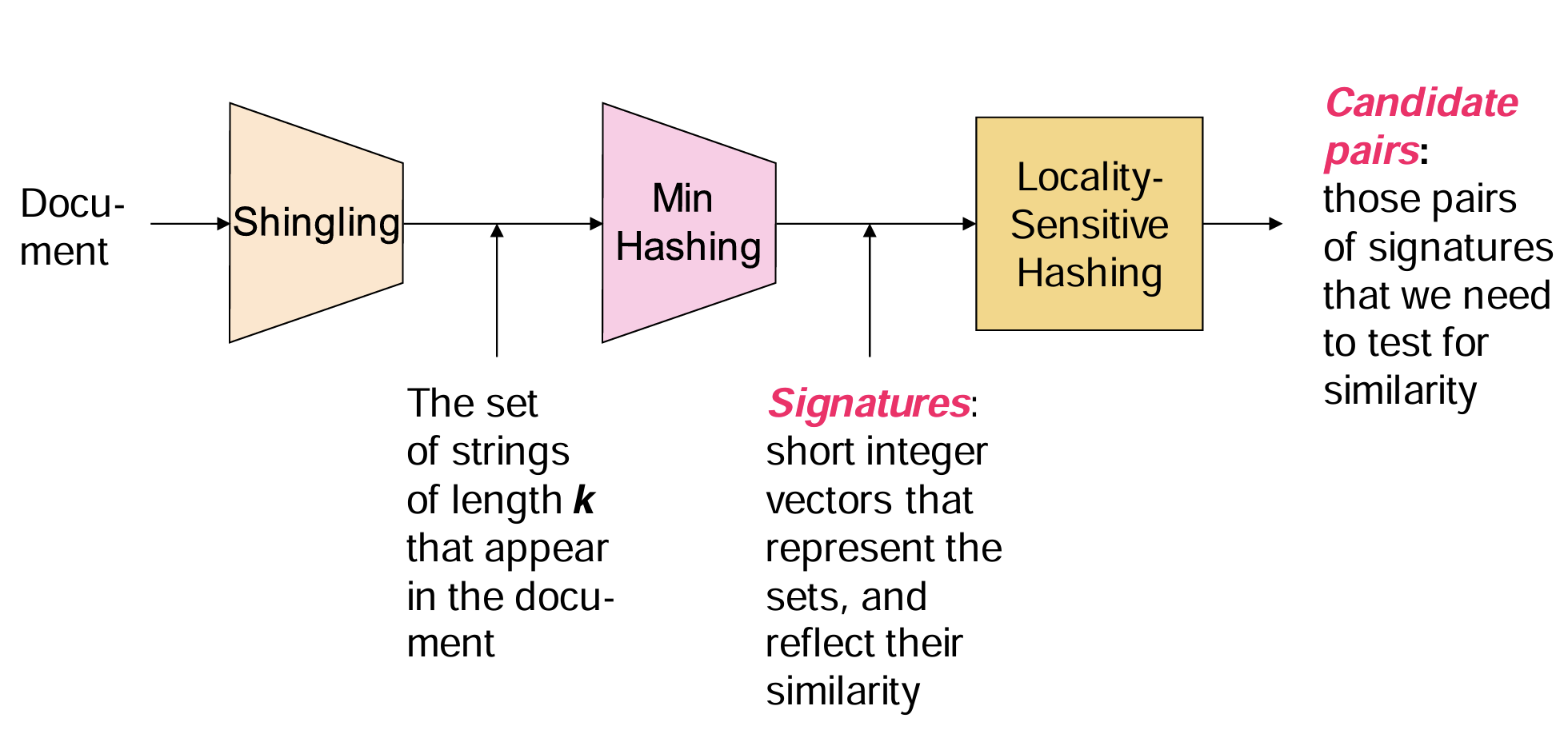三个步骤：
1. Shingling（n-gram特征提取）
  定义: Shingling是将文档转换为一个集合表示的过程，这个集合由文档中的特征（通常是n-gram或k-shingle）构成。
  - n-gram: 指文档中连续的n个字符或n个单词序列。例如，对于文本 “chatgpt is cool”，若n=3的字符shingle包括 “cha”, “hat”, “atg”, “tgp”, “gpt”, “pt “, “t i”, “ is”, “is “, “s c”, “ co”, “coo”, “ool”。
  - 集合表示: 每个文档都可以被表示为这些n-gram的集合。通过这种方式，不同文档中相同的n-gram可以反映它们之间的相似性。这种集合表示可以转换为布尔向量，其中向量的每一维表示一个n-gram是否存在于文档中。
  目标: 将文档表示为一个n-gram集合，以捕捉文档中局部的字符或词的相似性。通过这种表示，可以进一步进行相似性计算。
  
  优点包括：改变单个word只会影响其周围最多距离为1的特征；非常直观，具有相似内容的文档会有相同的n-gram特征。
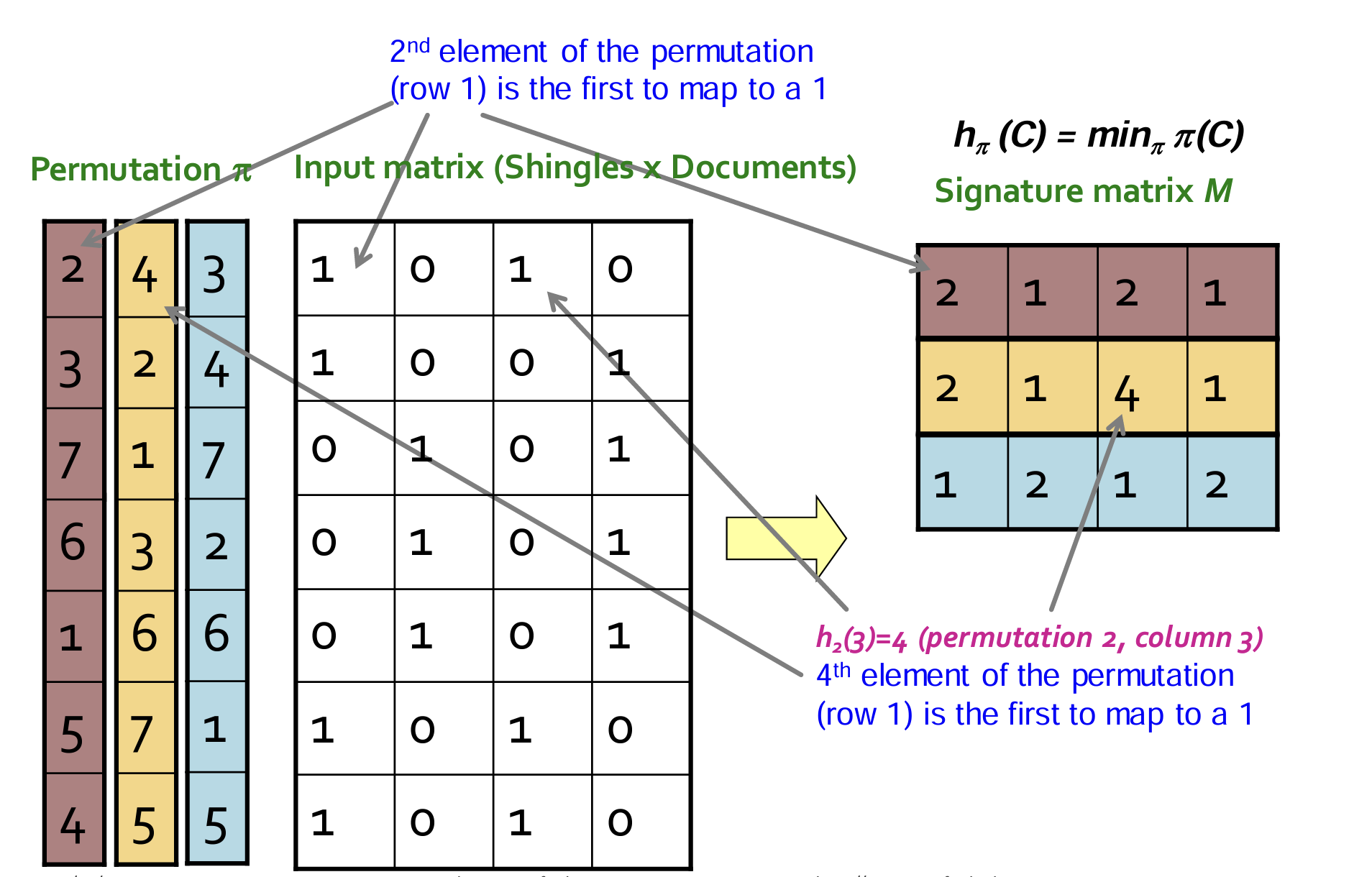
2. Min-Hashing
  定义: Min-Hashing是一种哈希技术，它将大的集合（如shingles集合）转换为短的签名（signature），同时保留集合之间的相似性特征。
  - 过程: Min-Hashing使用多个哈希函数，对每个文档的shingle集合进行哈希。对于每个哈希函数，它选择哈希值最小的shingle作为文档的“最小哈希值”（min-hash）。通过使用多种不同的哈希函数，可以为每个文档生成一个签名，即一个哈希值的向量。
  - 保留相似性: 如果两个文档相似，它们的shingle集合有较大的重叠，那么它们在多个哈希函数下得到相同最小哈希值的概率也会较高。因此，通过比较签名，可以近似地衡量两个文档之间的相似性。
    
    （低维度的签名能够保持相似性的原因如下图公式所示，假设其中的哈希函数$h_{\pi}$是一个序列变换，那么在进行序列变换后能够保持相同的概率即为其相似性）
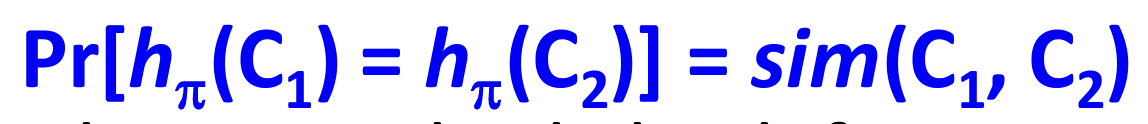
  目标: 将大的shingles集合转换为较短的签名，减少数据规模，同时保持文档之间的相似性特征。这使得在大规模数据集中进行相似性比较更加高效。
  - 如下图所示，Min-Hashing中的哈希函数使用的是Permutation序列变换；对于一个特定文档，例如matrix中的一列，运用一个序列变换后的最小的1值可以表征这个哈希函数对这个文档转换后的值。所以一个文档可以表征为#permutation维度的签名向量。
  - 从而实现一个 shingles集合bool向量转换为一个低维的签名的降维。
3. Locality-Sensitive Hashing (LSH)
  
  定义: LSH 是一种哈希技术，专注于将相似的签名（signature，签名在第二步min-hashing中已经实现）映射到同一个桶（bucket）中，使得相似的文档有更高的概率成为候选对（candidate pairs）。
  - 过程: LSH使用多组哈希函数，将Min-Hashing生成的签名映射到不同的桶中。每组哈希函数根据签名的不同部分进行哈希，以此确保相似的签名映射到相同桶中的概率较大。不同组哈希函数可以组合使用，进一步提高准确性。
  - 候选对: 通过LSH，将落在同一桶中的签名视为候选对。这些候选对可能来自相似的文档，因此只需对这些候选对进行进一步精确的相似性计算，而无需对所有文档进行两两比较。
  目标: 使用LSH，快速找到可能相似的文档对，大幅减少需要进行精确相似性计算的对数，从而提高大规模相似性检测的效率。
  
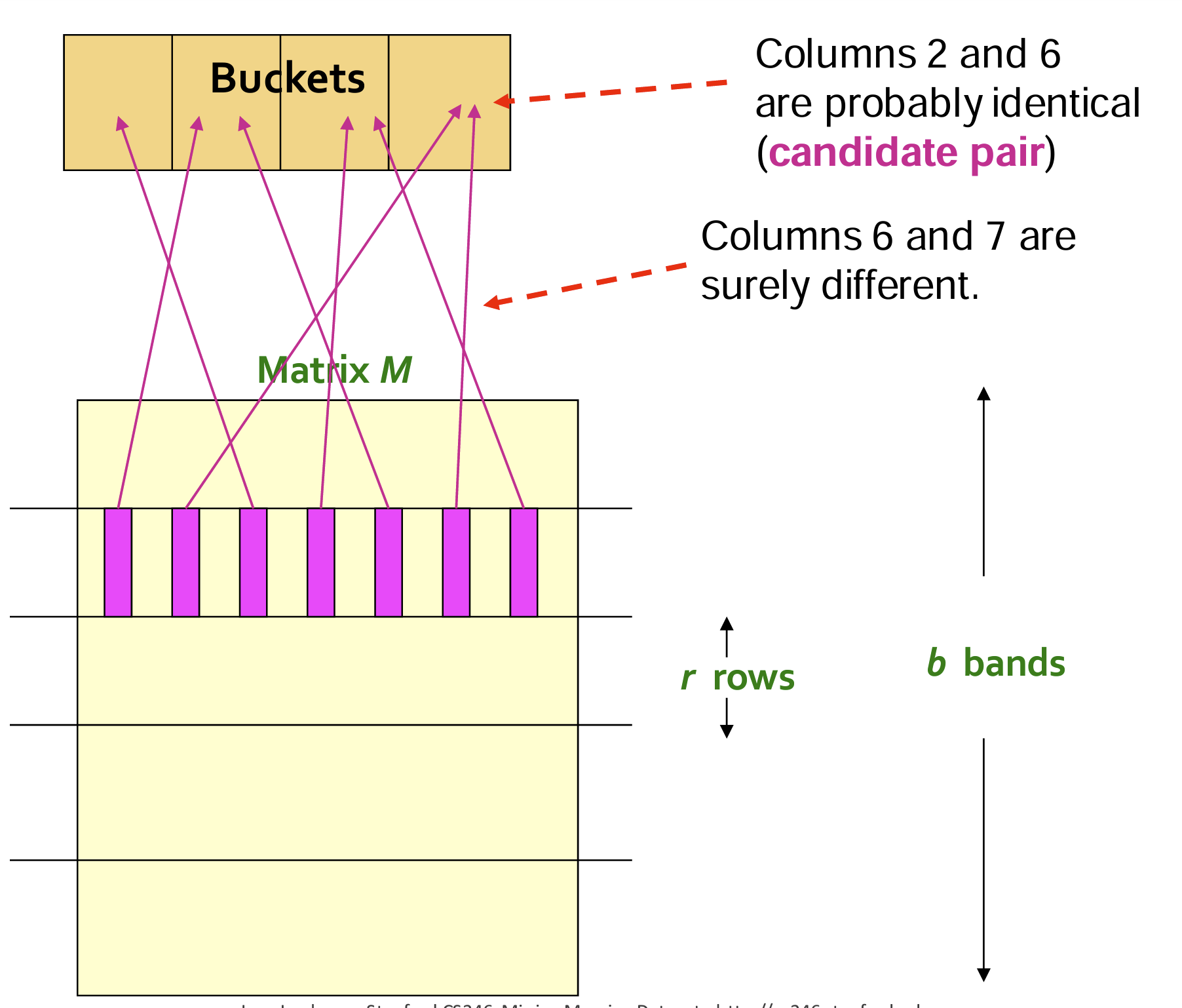
  如何处理min-hash矩阵？
  - 需要将min-hash矩阵划分为一个个band，对这些band进行单独的哈希映射。
  - 图解：

LSH算法误差

LSH算法是一个近似算法，不可避免的存在误差和错误。可以从概率的角度进行解释。
误差主要体现在两类错误上：误判（false positives）和漏判（false negatives）。

漏判（false negatives）

1. 目标是找到相似度大于0.8的doc pair，其中每一个bond有5行，一共有20个bonds。
2. 假设文档C1和C2在相似性为0.8的前提假设下，计算漏判false negatives的概率如下所示：（即计算两个文档在20个bonds中没有任何一个bond被划分入同一个bucket的概率）
3. 概率：即只有0.035%的概率存在漏判的可能。

误判（false positives）

1. 假设文档C1和C2在相似性为0.3的前提假设下，计算误判（false positives）的概率如下所示：（即计算两个文档在20个bonds中存在任何一个bond被划分入同一个bucket的概率）
2. 概率：有4.74%的可能性存在误判。

抉择（Trade off）

通过调整 #band 以及 rows per band 可以调整 false positives 以及 false negatives 的概率。
但是这是一个trade off。
当降低#band时，rows per band 会上升，那么两个文档完全相同的可能性就会减少。那么FN概率显然上升，FP概率显然下降。

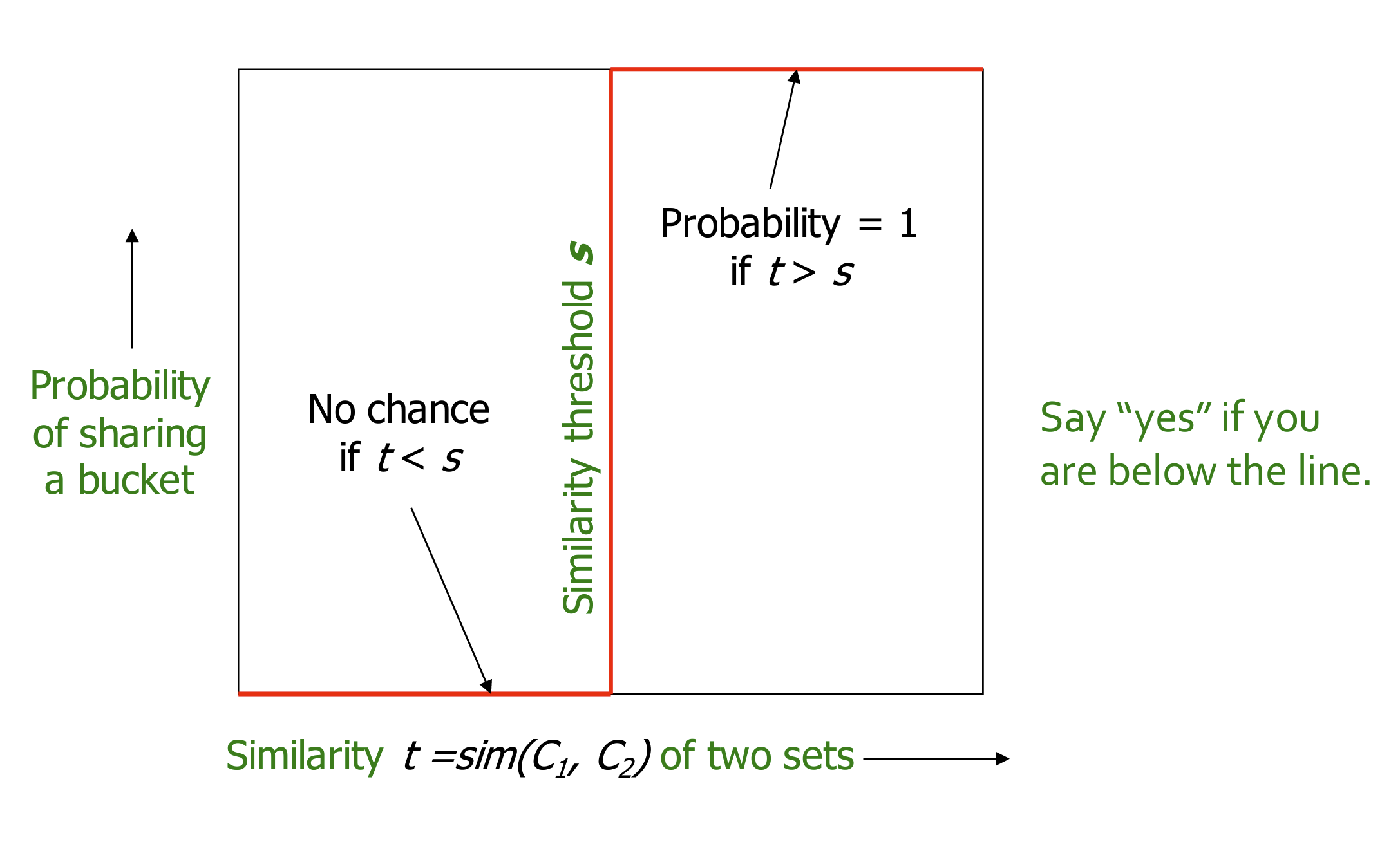
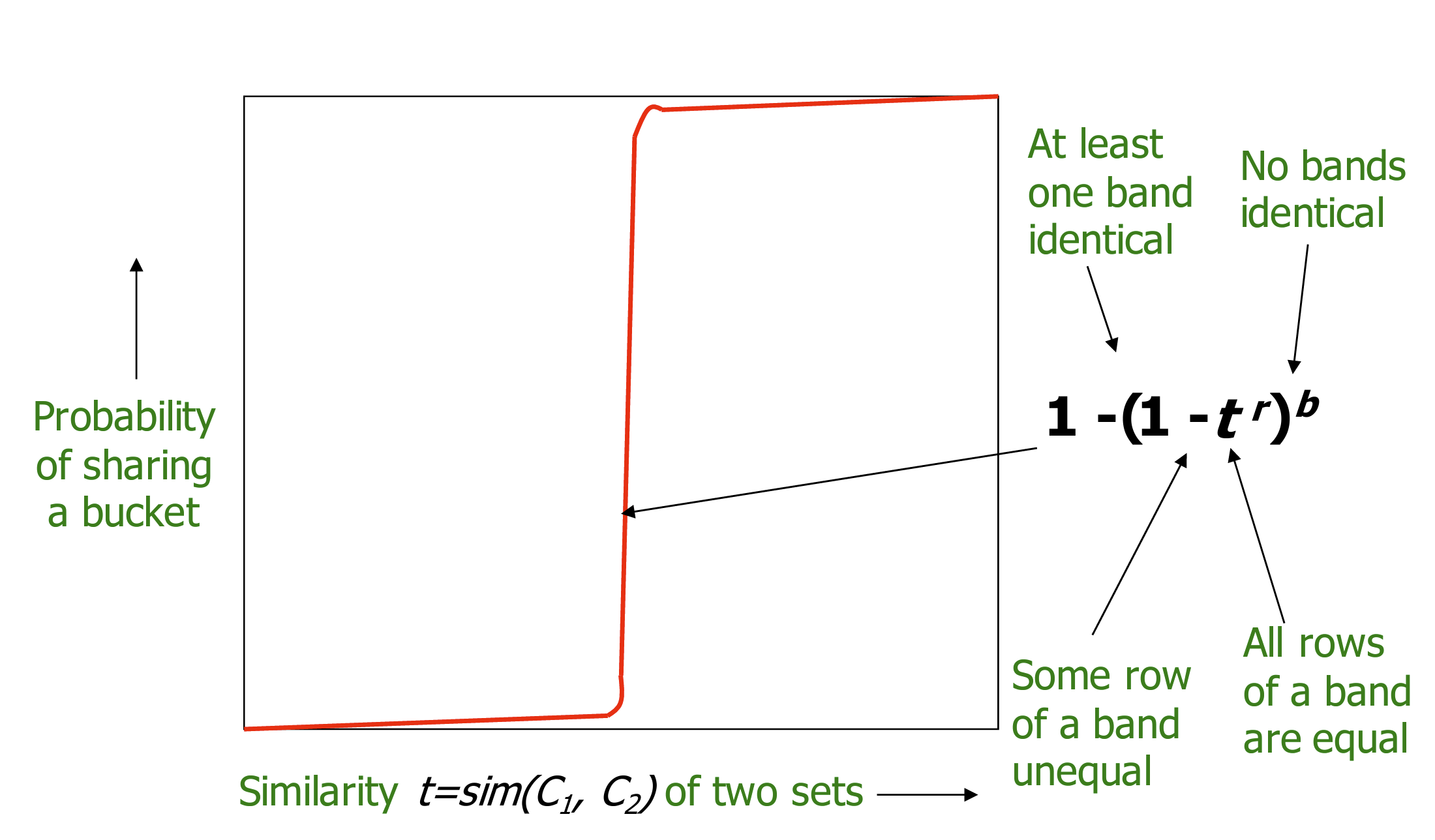
参数选择是一个重点

调整$b、r$ 来得到一个在指定的相似性阈值下的高效模型。

理想curve 以及实际 curve 如下图所示：

Section3.5: Theory of LSH

如何理解LSH的 Locality-Sensitive？

位置敏感，核心是位置（也解释points之间的距离）。如果两个对象在原始空间中距离足够接近，那么它们在散列空间中也有很高的概率被映射到相同的散列桶中。
重点内容：这是一个LSH的常用定义。

例如：Min-Hash的位置敏感性如下：

LSH在上述的内容用于文档的相似性检测，更加广泛地说：用于在一个巨大的稀疏矩阵中，找到Jaccard相似性高的columns
事实上，是一种 距离检测（使用的是Jaccard距离，即：

如何将LSH泛化到其他类型的距离？例如欧拉距离、cos距离等等。

LSH For Cos-distance：Random Hyperplanes

随机超平面 vs Min-Hash

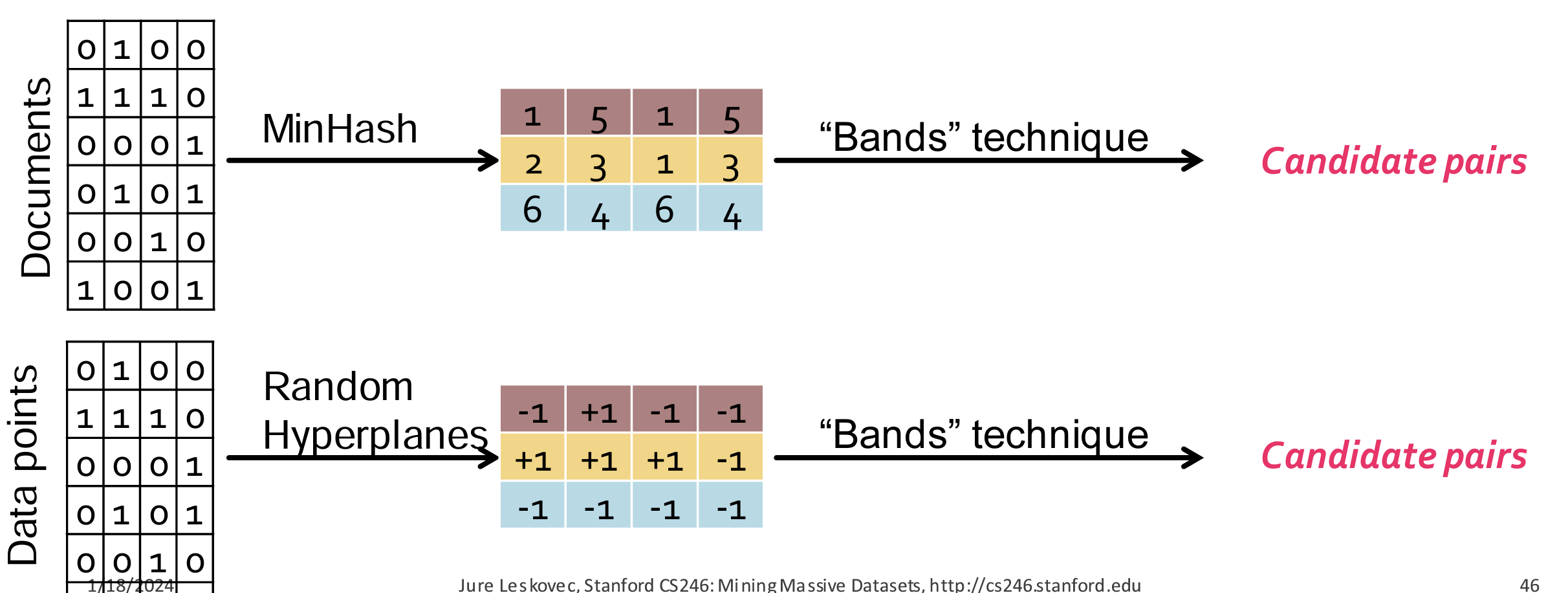
Random Hyperplanes 是一种用于 Locality-Sensitive Hashing (LSH) 的技术，主要应用于高维空间中的相似性搜索，特别是用于处理点之间的余弦相似度（Cosine Similarity）。其核心思想是利用随机生成的超平面将数据点划分到不同的区域，从而实现对数据点的分类和相似性判断。

工作原理

定义超平面：在 ( d ) 维空间中，一个超平面可以由一个法向量（即垂直于超平面的向量）来表示。通过随机生成多个法向量，我们可以定义多个超平面。
投影和分类：对于每个数据点，将其投影到由超平面定义的空间中。具体来说，计算数据点和超平面法向量的内积：
- 如果内积为正，则认为该点在超平面的“正”侧。
- 如果内积为负，则认为该点在超平面的“负”侧。
生成哈希签名：通过多个随机超平面来定义一组哈希函数，每个超平面对数据点产生一个比特值（正侧记为1，负侧记为0）。将这些比特值组合起来就得到了一个签名或哈希码。相似的点在这些超平面下有更高的概率生成相同的哈希码。
相似性判断：在查询时，将查询点通过相同的超平面集合进行哈希，得到哈希码。然后在哈希空间中查找具有相同或相似哈希码的点，从而实现高效的相似性搜索。

余弦距离

两个高维数据点之间的余弦距离就是两个向量之间的夹角(0-180度)

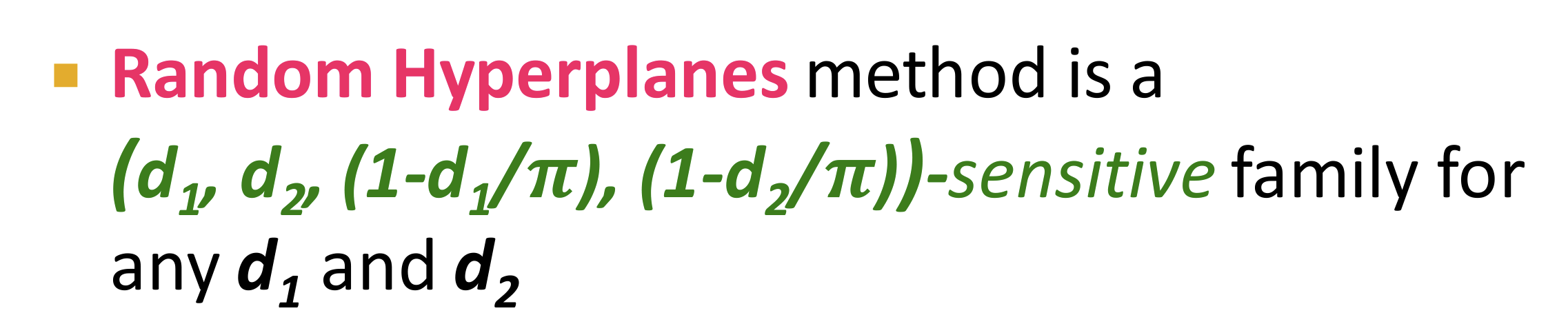
重点：将x和y哈希到随机超平面的同一边的概率就是其余弦相似性。

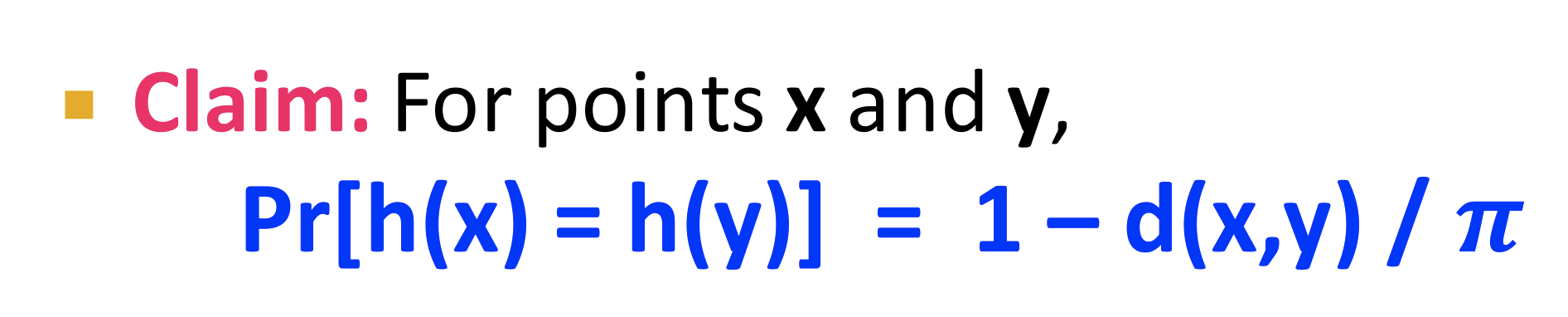
证明：只有随机超平面在两个向量之间的时候hash为-1，否则是+1；概率为$d(x,y)/\pi$

LSH For Euclidean Distance：Line Projection

主要的是思想是：哈希函数使用随机选择的一条直线，将数据点投影到该直线。在直线上定义散列桶，越接近的数据点散列到同一个桶的概率更高。

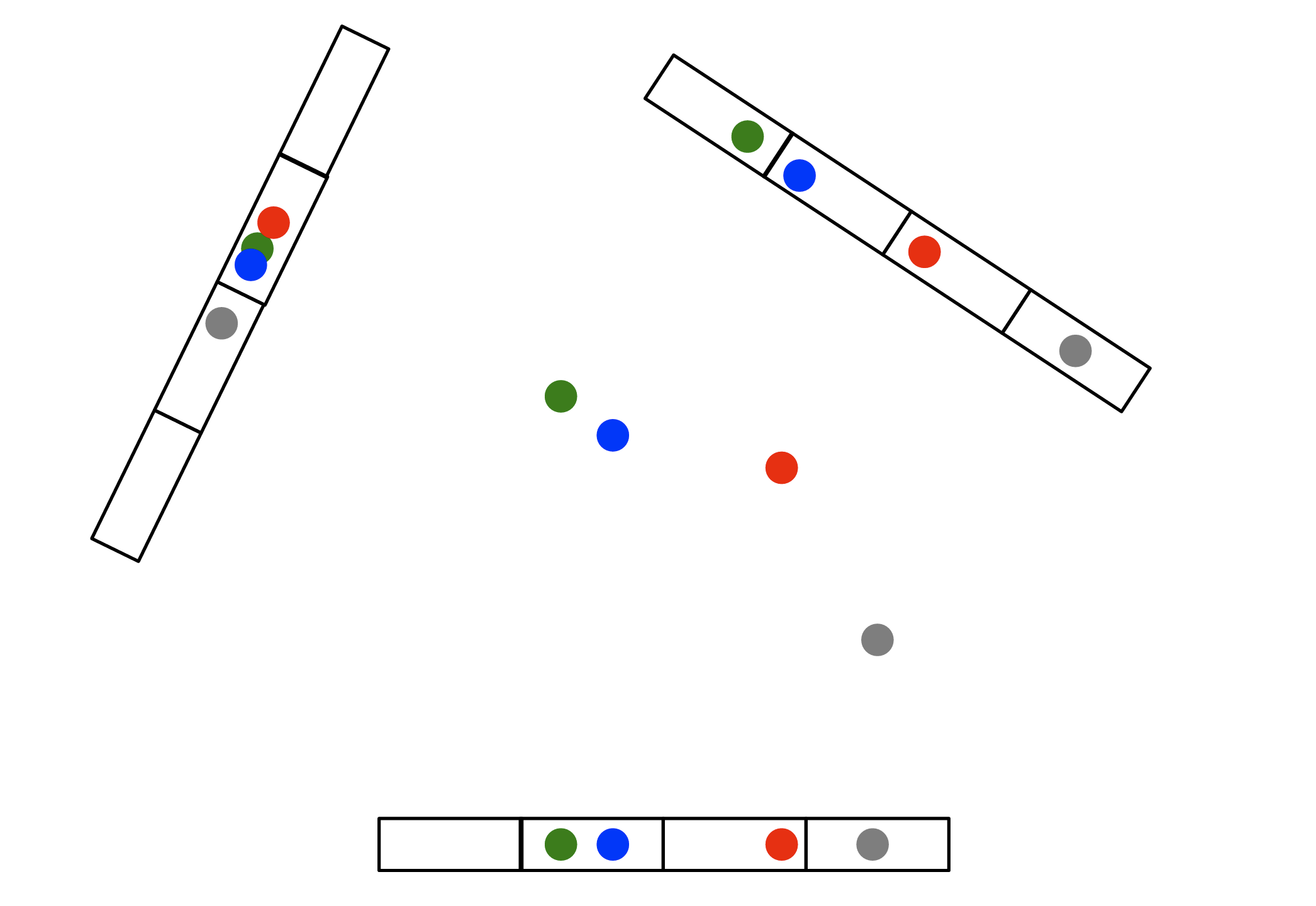
主要的步骤：

随机投影：选择一个随机方向（向量），即从一个高斯分布中随机抽取一个向量。这个随机向量用来定义一条投影线。
计算投影值：对于每个数据点，将其投影到这个随机向量上。计算该点在随机向量上的投影值，即点与随机向量的内积。
分配散列桶：将这些投影值划分为若干区间，每个区间对应一个散列桶。数据点根据它们的投影值落入相应的桶中。
重复多次：由于单一的随机投影不足以可靠地区分点的距离关系，因此通常会重复多次，使用多个随机投影向量，并组合它们的结果来形成最终的散列签名。

Section4: Clustering

思考：聚类和LSH的差异

既然都是将距离相近的点分到同一类别？那么它们有什么区别？
LSH核心在于 快速找到与给定点相似（相似性有不同定义）的点，适用于搜索和检索任务。尤其着重于在大规模的数据中进行搜索。
聚类的核心在于 全局数据的分组，发现数据的结构和模式，适用于模式识别，例如图像分割等等。
选择使用哪种方法取决于具体的应用需求：是要快速搜索相似项，还是要分析数据的内部结构。

聚类：overview

在聚类（Clustering）算法中，主要有两大类方法：层次聚类（Hierarchical Clustering）和点分配（Point Assignment）。

1. 层次聚类（Hierarchical Clustering）

层次聚类是一种通过构建层次结构来将数据分组的方法。它的结果通常以树状图（树状结构）表示，称为树状图（Dendrogram）。层次聚类可以进一步分为两种类型：

两种方式：bottom-up / top-down，即从数据点开始进行簇的聚合；或者是从一整个簇逐渐进行簇的分裂。

a. 聚合层次聚类（Agglomerative Hierarchical Clustering, Bottom-Up）

初始状态：每个数据点作为一个单独的簇，也就是说，假设有 ( n ) 个数据点，则开始时有 ( n ) 个簇。
操作过程：在每一步中，找到最近的两个簇，并将它们合并成一个簇。这种合并过程会重复进行，直到所有的数据点都被合并成一个簇为止。
合并准则：常用的“最近”定义包括最小距离（单链法）、最大距离（全链法）、平均距离等。
特点：这种方法是自底向上（bottom-up）的，因为它从每个数据点是单独一个簇开始，然后逐步合并直到只有一个簇。

b. 分裂层次聚类（Divisive Hierarchical Clustering, Top-Down）

初始状态：所有数据点最初作为一个单一的簇。
操作过程：在每一步中，将一个簇分裂成两个簇。这个过程会反复进行，直到每个数据点都被分割成单独的簇，或者达到了预定的簇数量。
分裂准则：可以使用各种方法来决定如何分裂一个簇，例如基于某些距离或密度的阈值。
特点：这种方法是自顶向下（top-down）的，因为它从一个大的簇开始，然后逐渐分裂成多个小簇。

层次聚类的主要问题？如何表达一个簇（clustr），如何定义簇之间的距离。

（1）使用重心或者簇心。

在欧拉空间的前提下，这个问题比较简单。一个簇可以使用重心表示，簇之间的距离例如重心距离、最短距离等。
注意，在欧拉空间中重心（Centroid）是有意义的；但是在非欧拉的环境中，重心可能无效。
非欧拉的前提下，一个簇可以使用其簇心（Clustroid ）表示，簇心一定是簇中存在的实际点。并且簇心到簇内其他点的距离最近（相似度最高）。

（2）直接将一个簇表示为数据点的集合

簇之间的距离使用：
1. 两个集合每个点之间的平均距离（即对两个簇的每个点都计算距离并平均）。
2. 集合之间的点的最大距离。
3. …..

如何选择不同的聚类方法和距离类型？

不同的聚类任务适用不同的方法，例如convex clustring适用于基于重心的聚类。
但是如下的案例不适用，反而适合使用基于簇之间点的最短距离进行聚类。

什么时候结束聚类？

设置临界阈值；在某些标志出现时停止（例如将两个相似性很差的簇聚在一起时）

k-means 算法

优点：
1. 计算效率高：在大数据集上，k-means 算法的计算复杂度较低，通常可以快速收敛。
缺点：
1. **需要预先指定 $k$**：算法要求用户预先指定簇的数量 $k$，在实际应用中，这个信息通常是未知的。
  - 肘部法（Elbow Method） （使用平均簇心距离-k曲线的肘点）
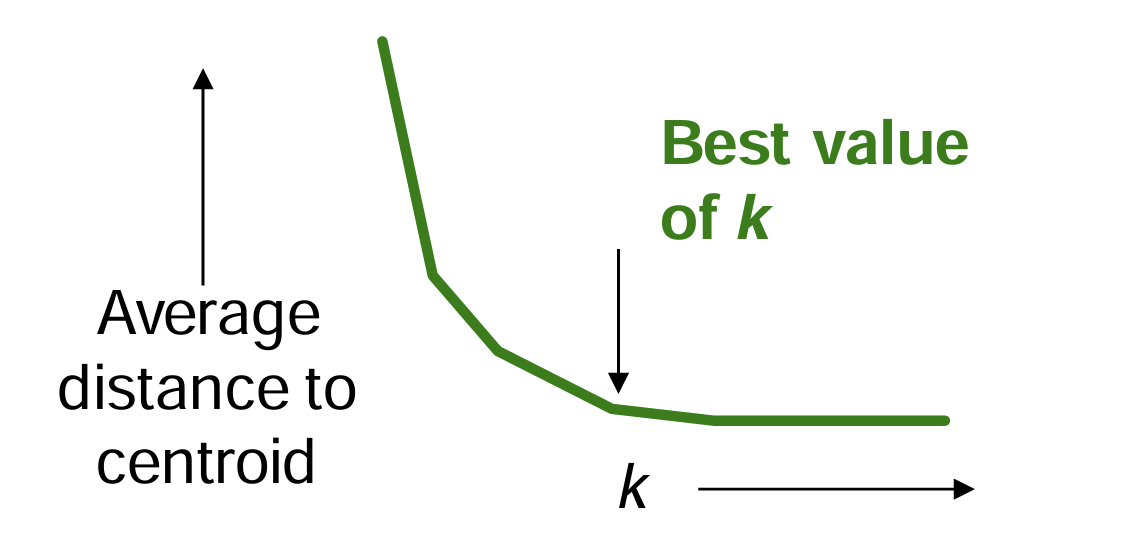
2. 对初始质心敏感：不同的初始质心选择可能导致不同的聚类结果，因此需要多次运行以获得更稳定的结果。
  - 改进：k-means++，使得选择较为分散的初始质心，以减少局部最优解的概率。
3. 易受离群点影响：离群点可能会极大地影响质心的计算，从而影响聚类结果。
4. 只能找到凸形簇：k-means 假设簇是球形的，对于非球形或复杂形状的簇，效果不佳。
  - 解决方法：下述的 CURE 算法

拓展k-means到大规模数据：BFR算法

BFR (Bradley-Fayyad-Reina) 算法是一种针对大规模高维数据集的聚类算法，主要的设计目标是处理存储在磁盘上的大量数据，这些数据无法一次性装入内存。
主要使用的方法：
1. 为了表示一个簇而不用记录这个簇的所有点，使用总结统计量（sufficient statistics）来表示每个簇
  - $N$：簇中点的数量。
    
    $SUM
    $：簇中所有点的坐标向量之和。自身也是一个向量。
    
    $SUMSQ$：簇中所有点的坐标向量平方和。自身也是一个向量。
  - 这些统计量允许计算簇的质心和方差(例如质心就是 $SUM/N$)，而无需存储所有点的具体坐标。
2. 三类集合：
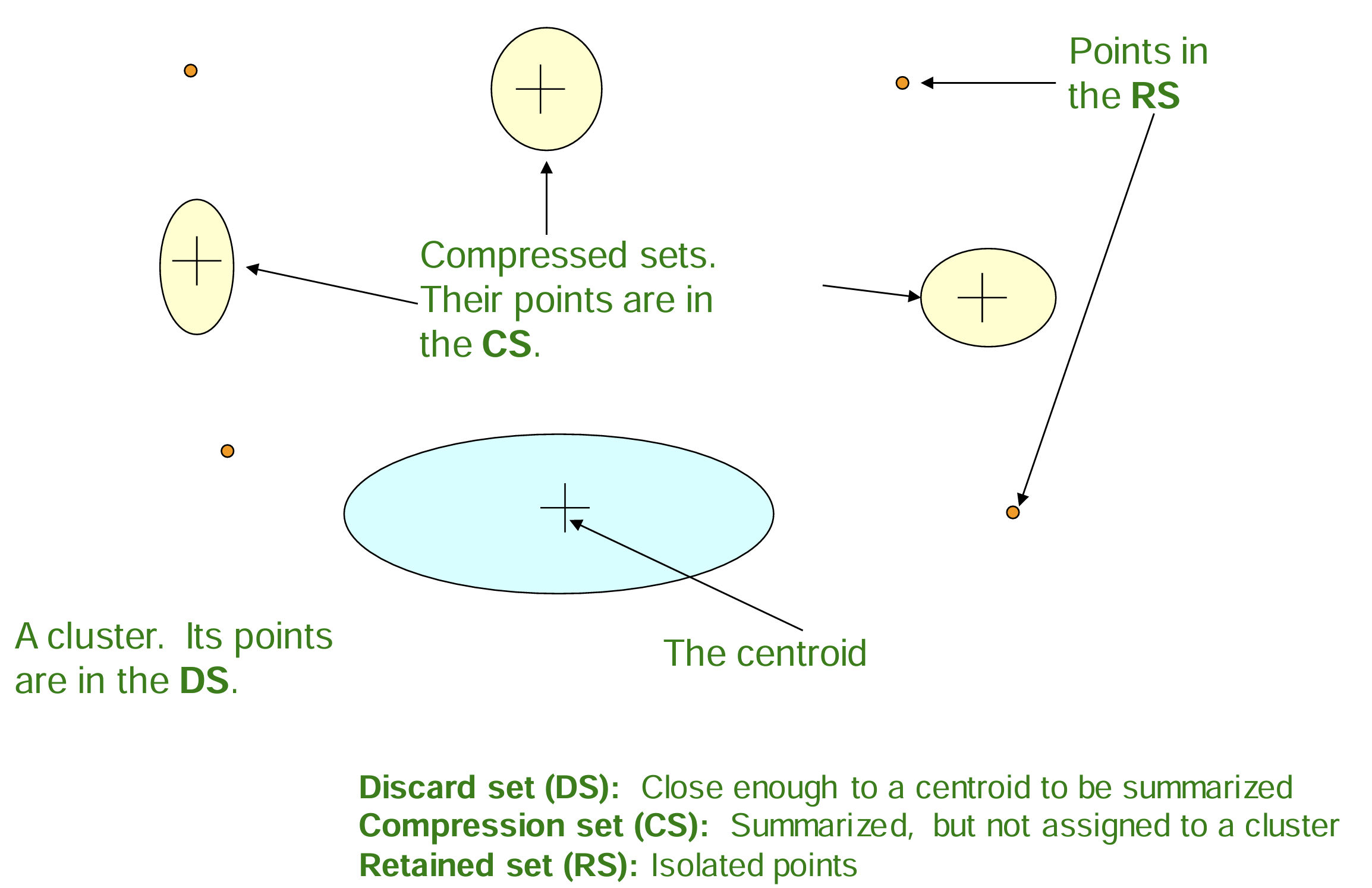
  - Discard Set （DS）：包含已经明确分配到某个簇中的点的统计量。
  - Compression Set （CS）：包含在当前批次中相互接近，但尚未明确分配到某个簇的点。这些点也使用总结统计量来表示。
  - Retained Set （RS）：离群点或噪声点，无法明确分配到任何簇。RS 中的点被保留，以便在后续批次中进行进一步处理。
BFR 算法的步骤
1. 初始化：
  - 随机选择一个小样本数据来初始化 $k$ 个簇。
  - 计算初始的 DS，并计算每个簇的统计量。
2. 处理每一批数据：
  - 从磁盘读取下一批数据点。
  - 对于每个数据点，计算它到现有 DS 中所有簇的距离：
    - 如果点距离某个簇的质心足够近，将点分配到该簇，更新 DS 的统计量。
      - 这里有一个问题：即多接近算是足够近？
        
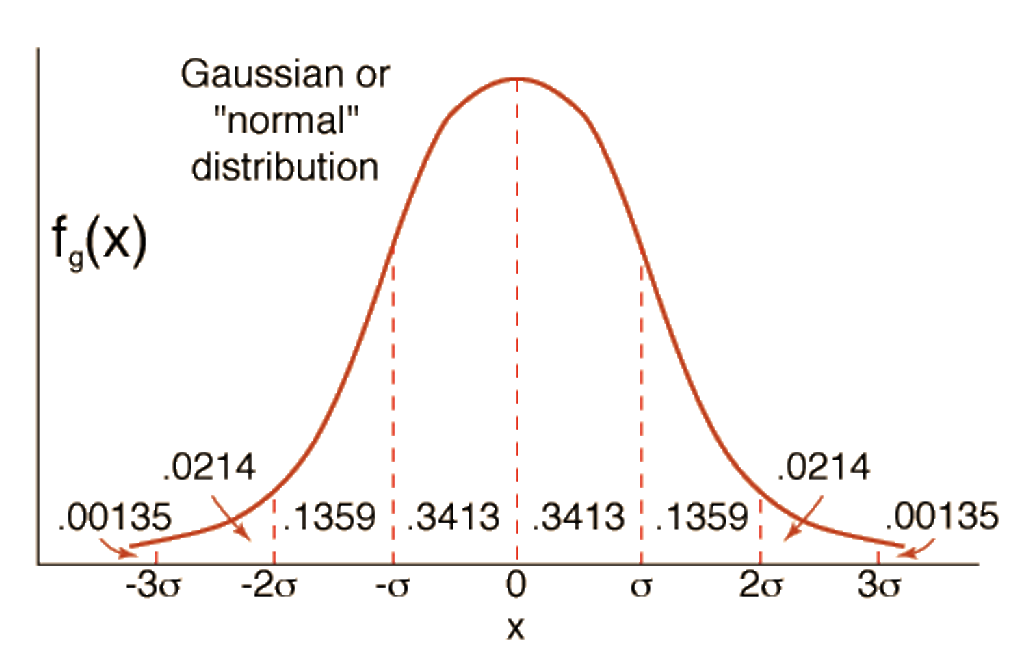
        High likelihood of the point belonging to currently nearest centroid【似然概率】；可以将一个簇进行看作一个正态分布，设置一个似然度阈值，例如距离为两个标准差之内的点算是“足够近”。
    - 如果点不能分配到任何簇，则考虑将其添加到 CS 中。
    - 如果点既不适合 DS 也不适合 CS，将其保留在 RS 中。
3. 处理 CS 和 RS：
  - 定期检查 CS 中的簇，如果发现两个簇足够接近，将它们合并。
  - 如果 RS 中的点可以形成新的簇，则将这些点移动到 CS 中。
4. 结束条件：
  - 当所有批次的数据都处理完时，检查 CS 和 RS，将它们中的点合并到最终的簇中。

CURE算法

Clustering Using Representatives。
主要用途：解决 k-means对于非球形或复杂形状的簇效果不佳的问题，可以把聚类扩展到不同形状的簇。
主要思想：
1. k-means使用一个簇的簇心（质心）来表示一个簇和合并簇，但是使用簇心只能发现球形的簇；CURE使用簇内的一组代表点来表示一个簇，从而可以体现这个簇的形状，而不仅限于球形簇。
2. 选择代表点时会选择簇内距离最远的几个点，可能受到离群点的影响。对代表点向簇心缩放一定比例，有利于抗离群点影响。
算法流程：

总结：使用代表点来表征一个簇的形状，并使用了点向簇心的缩放来抗离群点干扰。

Section5: Dimensionality Reduction

数据可以通过选择轴（axis）的方向进行投影进行降维

主要通过矩阵分解的方法对数据进行降维。

SVD分解

详细笔记见《统计学习方法》第15章

前置知识：矩阵的特征分解、对角化；正交矩阵；

数学表示

假设我们有一个 $m \times n$ 的矩阵 $A$，它可以被分解为三个矩阵的乘积：

$A = U \Sigma V^T$

$U$：一个$m \times m$的正交矩阵，其列向量称为左奇异向量。这个矩阵表示的是原始数据在新的正交基上的表示。
$\Sigma$：一个 $m \times n$ 的对角矩阵，对角线上是奇异值，非对角线元素全为零。奇异值表示矩阵在某些方向上的重要性或信息量，通常按降序排列。
$V^T$：一个 $n \times n$ 的正交矩阵，其行向量称为右奇异向量。这个矩阵对应的是数据在列空间中的正交表示。

性质

任何实矩阵的SVD分解一定存在，但是不唯一。
根据保留的奇异值的个数可以分为完全SVD、紧SVD、截断SVD
- 完全SVD：如数学表示中的公式所示，$\Sigma$ 的shape为 $m \times n$
- 紧SVD ：只保留非零的奇异值以及对应的奇异向量部分（即保留的奇异值个数等于原矩阵的秩）；紧SVD去除了冗余的零奇异值及其对应的奇异向量，使得分解更加紧凑，但仍然能够准确表示原矩阵。
- 截断SVD：仅保留前 $k$ 个最大的奇异值及其对应的奇异向量，形成一个近似矩阵。

SVD的几何解释

所有的矩阵都代表一个线性变换。
根据SVD的分解公式：将一个线性变换$A$ 分解为三个连续的等价变换（旋转、伸缩、再旋转）
$$
A = U \Sigma V^T
$$

计算过程

核心是计算$A^TA$，原因是：$A^TA$是一个实对称矩阵，可以进行特征分解（对角化）
$$
A^TA = V\Sigma^TU^T \times U \Sigma V^T = V \Sigma^2 V^T
$$
所以$\Sigma^2$等价于特征值对角矩阵，所以矩阵$A$奇异值是$A^TA$特征值的平方根。
如上公式可以求出正交矩阵$V^T$ 和对角矩阵$\Sigma$
现在高效的SVD的数值计算方法通常使用$A^TA$的特征值进行计算，但不直接计算$A^TA$

如何使用SVD进行数据降维

对数据矩阵进行SVD分解后，选择前$k$个奇异值和对应的奇异向量（丢弃较小的奇异值和奇异向量）。因为奇异值越大，表示在该方向上的方差越大，这个方向就越重要。
如何决定保留$k$的大小？保留一定 energy （信息）的数据。奇异值的平方表征特征值，其绝对大小可以表示energy的多少。

SVD缺陷

可解释性差：奇异值和奇异向量难以解释：虽然 SVD 提供了数据的最佳低秩近似，但奇异值和奇异向量通常缺乏直观的解释性。特别是在涉及实际应用的数据分析中，理解这些向量在原始问题中的含义可能非常困难。
- 可解释性较差：对于SVD分解，大家通常的理解应该是，左奇异向量以及右奇异向量分别张成了原始矩阵所在的列空间以及行空间，但是对于原始矩阵而言，并没有较强的可解释性。
SVD 在分解稀疏矩阵时通常会生成稠密矩阵，这意味着稀疏矩阵的稀疏性会丢失。在需要保持稀疏结构的应用中（例如某些大规模推荐系统或图像处理任务），这种稠密化可能带来存储和计算上的额外开销。
- 稀疏矩阵的稀疏性可以使得其在存储和计算的时候更加高效，在矩阵分解时保持稀疏性很有意义。
- 稠密化现象：即使原始矩阵 A 是稀疏矩阵，分解得到的 $U$、$\Sigma$ 和 $V$ 通常都是稠密矩阵。这是因为奇异值分解是基于全局信息进行的，不仅考虑了非零元素，还考虑了所有零元素的影响。
- 结果矩阵稠密化：当你使用 SVD 来近似重构矩阵 A 时，得到的矩阵通常也是稠密的。这意味着，在计算结果中，许多原本为零的元素会变成非零值，导致矩阵稀疏性丢失。

CUR分解

CUR分解是一种矩阵分解方法，主要用于稀疏矩阵的近似。与奇异值分解（SVD）不同，CUR分解通过从原始矩阵中直接选取实际的行和列来进行分解，从而更好地保持原始矩阵的稀疏性和可解释性。
为什么 CUR分解可行？
- 对于一个低秩或近似低秩的矩阵 $A$，可以用较少的特征信息来重构或近似这个矩阵。通常，低秩近似问题可以通过选择原始矩阵中的一些代表性行和列来解决。CUR分解就是基于这个思想，通过选取矩阵的一部分行和列来近似整个矩阵。

数学表示

对于一个矩阵 $A$，CUR分解将其分解为三个矩阵的乘积形式：
$$
A \approx C U R
$$
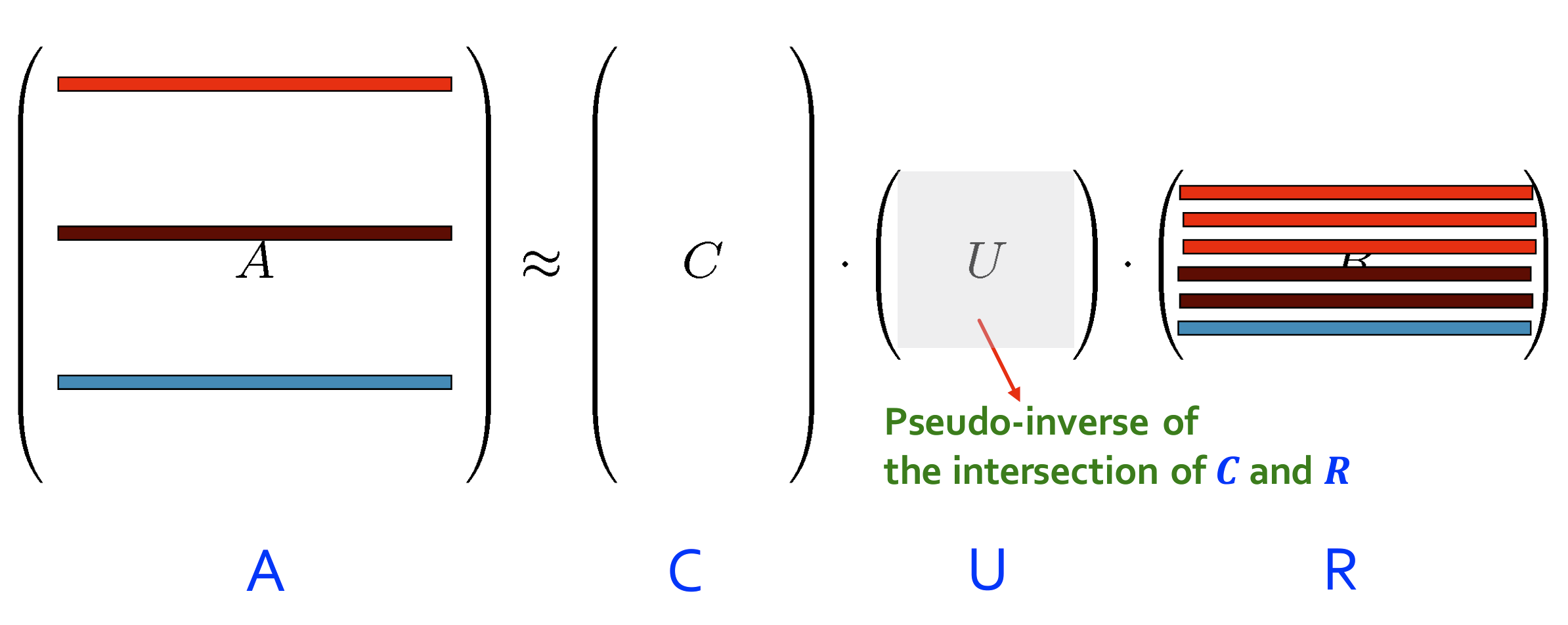
截屏2024-09-04 18.17.51

其中：

( C ) 是从矩阵 ( A ) 中选取的若干列组成的矩阵。
( R ) 是从矩阵 ( A ) 中选取的若干行组成的矩阵。
( U ) 是一个较小的核矩阵，它通过 ( C ) 和 ( R ) 的交集计算得到。

算法步骤

列选择（C 矩阵）：从原始矩阵 ( A ) 中随机或基于某种策略选取若干列，组成矩阵 ( C )。
行选择（R 矩阵）：从原始矩阵 ( A ) 中随机或基于某种策略选取若干行，组成矩阵 ( R )。
计算核矩阵 U：核矩阵 ( U ) 是通过 ( C ) 和 ( R ) 的交集（即从 ( C ) 的列和 ( R ) 的行组成的子矩阵）进行伪逆计算得到的。

矩阵 $U$ 的计算

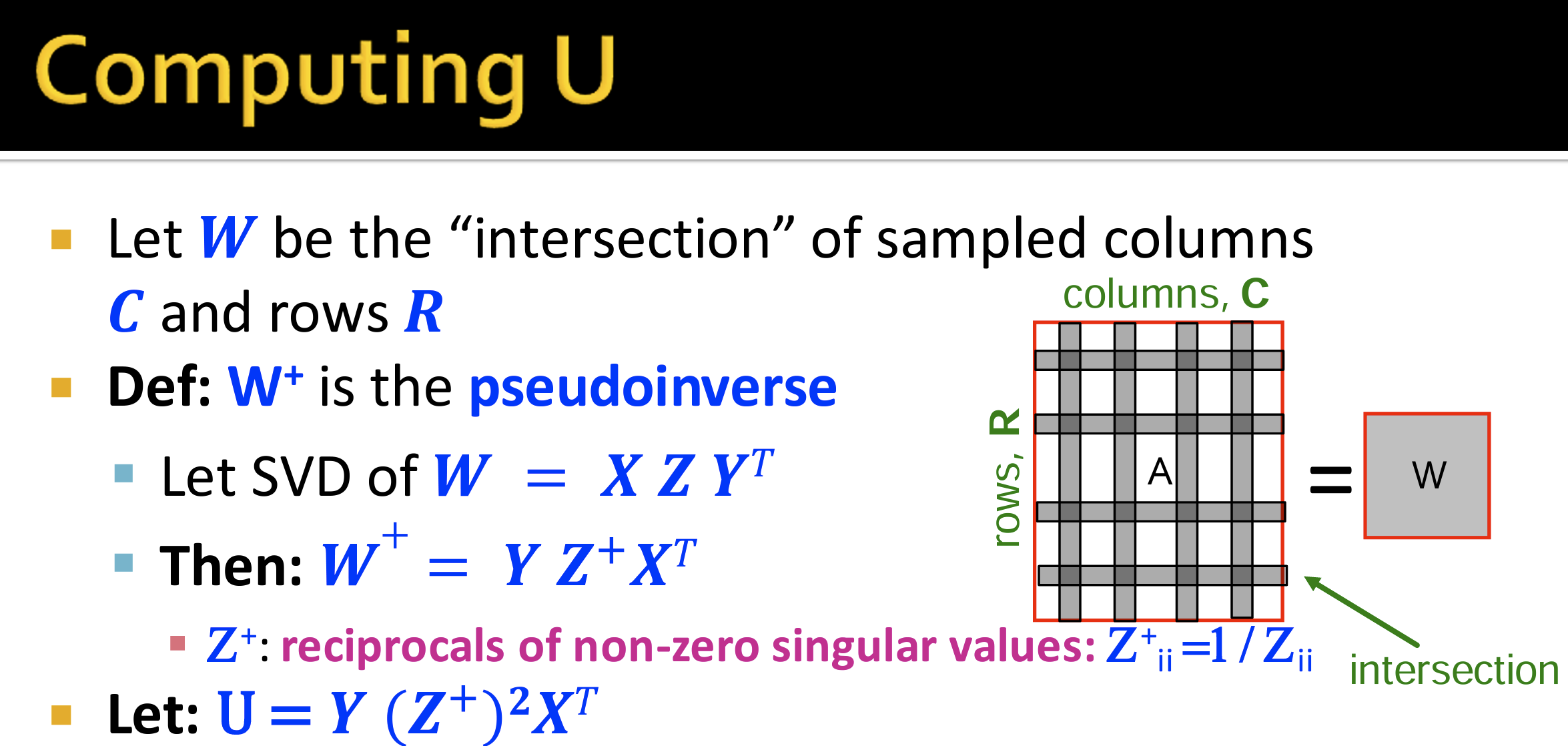
具体而言，假设 $W$ 是从 $A$ 中选择的行和列的交集部分，即：

$$
W = A(I, J)
$$

其中$I $ 是选择的行索引，$J$是选择的列索引，那么：

$$
U = W^+
$$

其中 $W^+$ 是 $W$ 的伪逆。

如何采样原始矩阵中的行/列？

随机采样，元素平方和较大的行/列采样的概率大。即将其二范数的占比作为其影响力的指标。
主要，这里是随机进行采样，同一行/列是有可能被采样不止一次的。

CUR 分解的可解释性

由于 CUR 分解中的 $C$ 和 $R$ 矩阵直接取自原始数据，领域专家或数据分析师可以轻松地将这些行和列映射回原始数据集，从而更好地理解和解释结果。例如：
- 在推荐系统中，$C$ 矩阵可以代表推荐系统中挑选出的代表性物品，而 $R$ 矩阵可以代表挑选出的用户。这使得结果可以直接解释为哪些物品和用户在整个数据集中最具代表性。

CS246: Mining Massive Data Sets

大数据挖掘

Section0：Intruduction

Section1： MapReduce and Spark

分布式计算

MapReduce

Spark：对MapReduce的扩展

MapReduce应用

Section2：Frequent Itemsets Mining & Association Rule

频繁项集挖掘 和 关联规则

1. Items（项目）

2. Baskets（篮子）

Frequent Itemsets Mining

Association Rule

评价指标

如何找到关联规则？

A-priori 算法

更多算法

Section3: Locality-Sensitive Hashing

文档相似性检测

如何定义文档之间的相似性？

Shingling（n-gram特征提取）

Min-Hashing

Locality-Sensitive Hashing (LSH)

如何处理min-hash矩阵？

LSH算法误差

漏判（false negatives）

误判（false positives）

抉择（Trade off）

参数选择是一个重点

Section3.5: Theory of LSH

如何理解LSH的 Locality-Sensitive？

LSH For Cos-distance：Random Hyperplanes

工作原理

余弦距离

LSH For Euclidean Distance：Line Projection

主要的步骤：

Section4: Clustering

思考：聚类和LSH的差异

聚类：overview

1. 层次聚类（Hierarchical Clustering）

如何选择不同的聚类方法和距离类型？

什么时候结束聚类？

k-means 算法

拓展k-means到大规模数据：BFR算法

CURE算法

Section5: Dimensionality Reduction

SVD分解

数学表示

性质

SVD的几何解释

计算过程

如何使用SVD进行数据降维

SVD缺陷

CUR分解

数学表示

算法步骤

矩阵 $U$ 的计算

如何采样原始矩阵中的行/列？

CUR 分解的可解释性

频繁项集挖掘和关联规则